How can I score full marks in the Statistics questions in exams?

  $\left|\frac{1}{2}-2i+1\right|=\alpha \left(\frac{1}{2}-2i\right)+\beta \left(1+i\right)$  

$\sqrt[]{\frac{9}{4}+4}=\alpha \left(\frac{1}{2}-2i\right)+\beta \left(1+i\right)$

$\frac{5}{2}=\alpha \left(\frac{1}{2}\right)+\beta +i\left(-2\alpha +\beta \right)$             

$\frac{\alpha }{2}+\beta =\frac{5}{2}$      ...(1)

 –2α + β = 0                    …(2)

Solving (1) and (2)

$\frac{\alpha }{2}+2\alpha =\frac{5}{2}$

$\frac{5}{2}\alpha =\frac{5}{2}$            

a =

Start with

(1) $\overline{E}:\frac{6!}{2!}=360$  

(2)    $\overline{GE}:\frac{5!}{2!},$ $\overline{GN}:\frac{5!}{2!}$  

(3) GTE : 4!, GTN: 4!, GTT : 4!

(4) GTWENTY = 1

⇒ 360 + 60 + 60 + 24 + 24 + 24 + 1 = 553

$f\left(x\right)=\{\begin{array}{cc}\hfill 2+2x,\hfill & \hfill x\in \left(-1,0\right)\hfill \\ \hfill 1-\frac{x}{3},\hfill & \hfill x\in [0,3)\hfill \end{array}$

$g\left(x\right)=\{\begin{array}{cc}\hfill x,\hfill & \hfill x\in [0,1)\hfill \\ \hfill -x,\hfill & \hfill x\in \left(-3,0\right)\hfill \end{array}$   ->g(x) = |x|, x Î (–3, 1)

$f\left(g\left(x\right)\right)=\{\begin{array}{cc}\hfill 2+2\left|x\right|,\hfill & \hfill \left|x\right|\in \left(-1,0\right)\Rightarrow x\in ?\hfill \\ \hfill 1-\frac{\left|x\right|}{3},\hfill & \hfill \left|x\right|\in [0,3)\Rightarrow x\in \left(-3,1\right)\hfill \end{array}$            

$f\left(g\left(x\right)\right)=\{\begin{array}{cc}\hfill 1-\frac{x}{3},\hfill & \hfill x\in [0,1)\hfill \\ \hfill 1+\frac{x}{3},\hfill & \hfill x\in \left(-3,0\right)\hfill \end{array}$

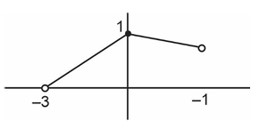
Range of fog(x) is [0, 1]

            Range of fog(x) is [0, 1]

First term = a

Common difference = d

Given: a + 5d = 2        . (1)

Product (P) = (a₁a₅a₄) = a (a + 4d) (a + 3d)

Using (1)

P = (2 – 5d) (2 – d) (2 – 2d)

-> = (2 – 5d) (2 –d) (– 2) + (2 – 5d) (2 – 2d) (– 1) + (– 5) (2 – d) (2 – 2d)

$\frac{dP}{dd}$ = –2 [ (d – 2) (5d – 2) + (d – 1) (5d – 2)

16cos²θ + 25sin²θ + 40sinθ cosθ = 1

16 + 9sin²θ + 20sin 2θ = 1

$16+9\left(\frac{1-cos2\theta }{2}\right)$            + 20sin 2θ = 1

$\frac{-9}{2}cos2\theta +20sin2\theta =\frac{-39}{2}$            

– 9cos 2θ + 40sin 2θ = – 39

$-9\left(\frac{1-ta{n}^2\theta }{1+ta{n}^2\theta }\right)+40\left(\frac{2tan\theta }{1+ta{n}^2\theta }\right)=-39$            

48tan²θ + 80tanθ + 30 = 0

24tan²θ + 40tanθ + 15 = 0

  $tan\theta =\frac{-40\pm \sqrt[]{{\left(40\right)}^2-15\times 24\times 4}}{2\times 24}$ &