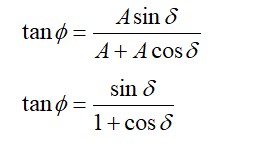A uniform rod, of mass , length and radius of cross section, is rotated about an axis passing through one of its ends and perpendicular to its length with constant angular velocity in horizontal plane. If is the Young's modulus of the material of rod, the increase in its length due to rotation of rod is
A uniform rod, of mass , length and radius of cross section, is rotated about an axis passing through one of its ends and perpendicular to its length with constant angular velocity in horizontal plane. If is the Young's modulus of the material of rod, the increase in its length due to rotation of rod is
Option 1 - <p><span class="mathml" contenteditable="false"> <math> <mfrac> <mrow> <mrow> <mi>m</mi> <msup> <mrow> <mrow> <mi>ω</mi> </mrow> </mrow> <mrow> <mrow> <mn>2</mn> </mrow> </mrow> </msup> <msup> <mrow> <mrow> <mi>L</mi> </mrow> </mrow> <mrow> <mrow> <mn>2</mn> </mrow> </mrow> </msup> </mrow> </mrow> <mrow> <mrow> <mi>π</mi> <msup> <mrow> <mrow> <mi>r</mi> </mrow> </mrow> <mrow> <mrow> <mn>2</mn> </mrow> </mrow> </msup> <mi>Y</mi> </mrow> </mrow> </mfrac> </math> </span></p>
Option 2 - <p><span class="mathml" contenteditable="false"> <math> <mfrac> <mrow> <mrow> <mi>m</mi> <msup> <mrow> <mrow> <mi>ω</mi> </mrow> </mrow> <mrow> <mrow> <mn>2</mn> </mrow> </mrow> </msup> <msup> <mrow> <mrow> <mi>L</mi> </mrow> </mrow> <mrow> <mrow> <mn>2</mn> </mrow> </mrow> </msup> </mrow> </mrow> <mrow> <mrow> <mn>2</mn> <mi>π</mi> <msup> <mrow> <mrow> <mi>r</mi> </mrow> </mrow> <mrow> <mrow> <mn>2</mn> </mrow> </mrow> </msup> <mi>Y</mi> </mrow> </mrow> </mfrac> </math> </span></p>
Option 3 - <p><span class="mathml" contenteditable="false"> <math> <mfrac> <mrow> <mrow> <mi>m</mi> <msup> <mrow> <mrow> <mi>ω</mi> </mrow> </mrow> <mrow> <mrow> <mn>2</mn> </mrow> </mrow> </msup> <msup> <mrow> <mrow> <mi>L</mi> </mrow> </mrow> <mrow> <mrow> <mn>2</mn> </mrow> </mrow> </msup> </mrow> </mrow> <mrow> <mrow> <mn>3</mn> <mi>π</mi> <msup> <mrow> <mrow> <mi>r</mi> </mrow> </mrow> <mrow> <mrow> <mn>2</mn> </mrow> </mrow> </msup> <mi>Y</mi> </mrow> </mrow> </mfrac> </math> </span></p>
Option 4 - <p><span class="mathml" contenteditable="false"> <math> <mfrac> <mrow> <mrow> <mn>2</mn> <mi>m</mi> <msup> <mrow> <mrow> <mi>ω</mi> </mrow> </mrow> <mrow> <mrow> <mn>2</mn> </mrow> </mrow> </msup> <msup> <mrow> <mrow> <mi>L</mi> </mrow> </mrow> <mrow> <mrow> <mn>2</mn> </mrow> </mrow> </msup> </mrow> </mrow> <mrow> <mrow> <mi>π</mi> <msup> <mrow> <mrow> <mi>r</mi> </mrow> </mrow> <mrow> <mrow> <mn>2</mn> </mrow> </mrow> </msup> <mi>Y</mi> </mrow> </mrow> </mfrac> </math> </span></p>
3 Views|Posted 5 months ago
Asked by Shiksha User
1 Answer
A
Answered by
5 months ago
Correct Option - 3
Detailed Solution:
Similar Questions for you
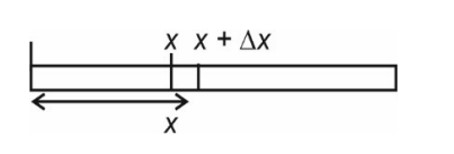
From A to B the process is isobaric
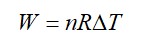
= W = 2 × R (600 - 350)
= 500 R
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else.
On Shiksha, get access to
66K
Colleges
|
1.2K
Exams
|
6.9L
Reviews
|
1.8M
Answers
Learn more about...

Physics Mechanical Properties of Solids 2025
View Exam DetailsMost viewed information
SummaryDidn't find the answer you were looking for?
Search from Shiksha's 1 lakh+ Topics
or
Ask Current Students, Alumni & our Experts
Have a question related to your career & education?
or
See what others like you are asking & answering