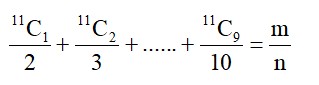C1 and C2 are two circles whose equations are given as x2 + y2 = 25 and x2 + y2 + 10x + 6y + 1 = 0. Now C3 is a variable circle which cuts C1 and C2 orthogonally. Tangents are drawn from the centre of C3 to C1, if the locus of the mid point of the chord of contact of tangents is ax + 3y + (where a, b Z+, and a and b are relative prime), then is
C1 and C2 are two circles whose equations are given as x2 + y2 = 25 and x2 + y2 + 10x + 6y + 1 = 0. Now C3 is a variable circle which cuts C1 and C2 orthogonally. Tangents are drawn from the centre of C3 to C1, if the locus of the mid point of the chord of contact of tangents is ax + 3y + (where a, b Z+, and a and b are relative prime), then is
Centre of C3 will lie on the radical axis of C1 and C2 which is 10x + 6y + 26 = 0.
Let center of C3 is (h, k).
Equation of chord of contact through (h, k) to the C1 may be given as hx + ky = 25 … (I)
Let the mid point of the chord is (x1, y1) the equation of the chord with the help of mid point may be
Similar Questions for you
...(1)
–2α + β = 0 …(2)
Solving (1) and (2)
a =
Variance =
α2 + β2 = 897.7 × 8
= 7181.6
Start with
(1)
(2)
(3) GTE : 4!, GTN: 4!, GTT : 4!
(4) GTWENTY = 1
⇒ 360 + 60 + 60 + 24 + 24 + 24 + 1 = 553
->g(x) = |x|, x Î (–3, 1)
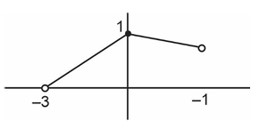
Range of fog(x) is [0, 1]
Range of fog(x) is [0, 1]
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else.
On Shiksha, get access to
Learn more about...

Maths Ncert Solutions class 11th 2026
View Exam DetailsMost viewed information
SummaryDidn't find the answer you were looking for?
Search from Shiksha's 1 lakh+ Topics
Ask Current Students, Alumni & our Experts
Have a question related to your career & education?
See what others like you are asking & answering