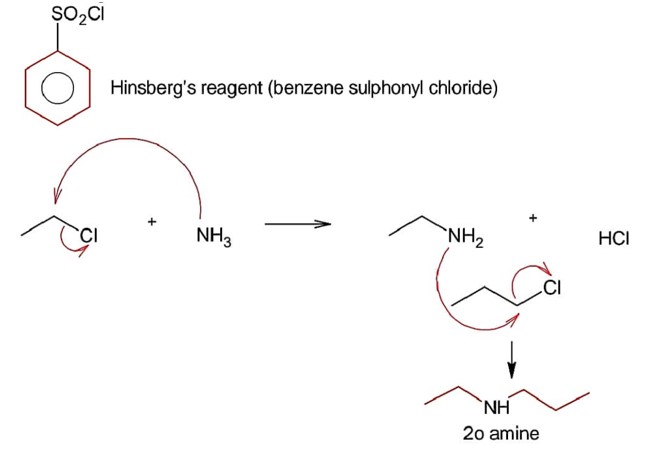
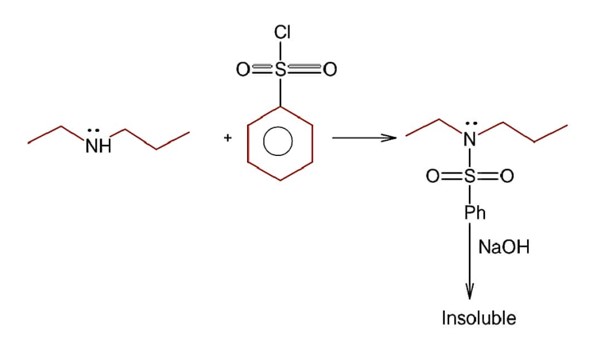
An amine on reaction with benzenesulphonyl chloride produces a compound insoluble in alkaline solution. This amine can be prepared by ammonolysis of ethyl chloride. The correct structure of amine is
An amine on reaction with benzenesulphonyl chloride produces a compound insoluble in alkaline solution. This amine can be prepared by ammonolysis of ethyl chloride. The correct structure of amine is
Option 1 -
Image 1
Option 2 -
Image 2
Option 3 -
Image 3
Option 4 -
Image 4
-
1 Answer
-
Correct Option - 4
Detailed Solution:Hinsberg test for amines
Similar Questions for you
In Amines, the nitrogen atom bonds with alkyl or aryl groups replacing hydrogen, whereas in amides, the nitrogen atom bonds directly with the carbonyl group (-CO-).
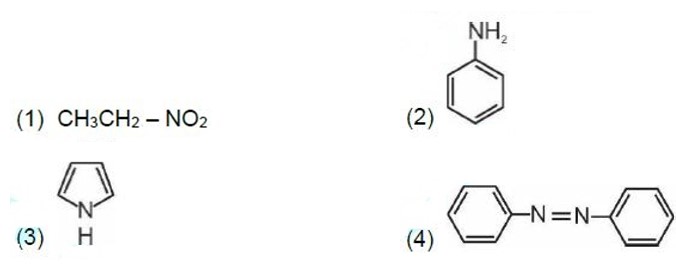
Kjeldahl's method is not applicable to compounds containing nitrogen in nitro and azo groups and nitrogen present in the ring.
Correct order of basic strength in aqueous medium is
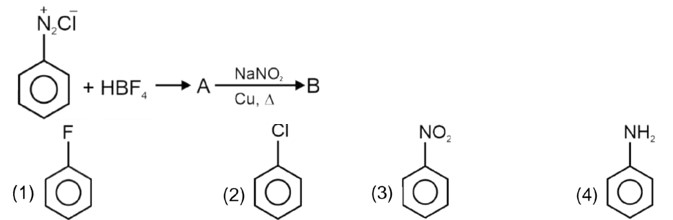
Kindly consider the following figure
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 65k Colleges
- 1.2k Exams
- 686k Reviews
- 1800k Answers