14. If a and b are distinct integers, prove that a – b is a factor of an– bn, whenever n is a positive integer. [Hint: write an= (a – b + b)n and expand]

14. For (a – b) to be a factor of an – b nwe need to show (an – bn) = (a – b)k as k is a natural number. We have, for positive n an = (a−b+b)n = [(a−b)+b]n =>an = nC0(a – b)n + nC1(a – b)n -1b + nC2(a – b)n – 2b2 + ………… +nCn-1 (a−b) bn−1 + nCnbn =>an= (a−b)n + nC1 (a−b)n−1 b + nC2 (a−b)n−2 b2 + …………….…+ nCn-1 (a−b) bn−1 + bn [Since, nC0 = 1 and nCn = 1] => an−bn = (a−b)n +nC1 (a−b)n−1 b + nC2 (a−b)n−2 b2 + ……………… + nCn-1 (a−b) bn−1 => an−bn = (a−b) [ (a−b)n−1 + nC1 (a−b)n−2 b + nC2 (a−b)n−3 b2 +………..…… + nCn-1 bn−1 ] => an−bn = (a−b) k where k = [ (a−b)n−1 + nC1 (a−b)n−2 b + nC2 (a−b)n−3 b2 +………..…… + nCn-1 bn−1 ] is a natural number. Therefore (a – b) is a factor of an – bnwhere n is positive integer.

14. If a and b are distinct integers, prove that a – b is a factor of aⁿ– bⁿ, whenever n is a positive integer.

[Hint: write aⁿ= (a – b + b)ⁿ and expand]

20 Views|Posted 8 months ago

Asked by Shiksha User

1 Answer

Sort by:

Answered by

Payal Gupta | Contributor-Level 10

8 months ago

14. For (a – b) to be a factor of aⁿ – b ⁿwe need to show (aⁿ – bⁿ) = (a – b)k as k is a natural number.

We have, for positive n

aⁿ = ${(a - b + b)}^{n}$ = ${[(a - b) + b]}^{n}$

=>aⁿ = ⁿC₀(a – b)ⁿ + ⁿC₁(a – b)^{n -}¹b + ⁿC₂(a – b)^{n –}²b² + ………… +ⁿC_n_-1 $(a - b) b^{n - 1}$ + ⁿC_nbⁿ

=>aⁿ= ${(a - b)}^{n}$ + ⁿC₁ ${(a - b)}^{n - 1} b$ + ⁿC₂ ${(a - b)}^{n - 2} b^{2}$ + …………….…+ ⁿC_n_-1 $(a - b) b^{n - 1}$ + $b^{n}$ [Since, ⁿC₀ = 1 and ⁿC_n = 1]

=> $a^{n} - b^{n}$ = ${(a - b)}^{n}$ +ⁿC₁ ${(a - b)}^{n - 1} b$ + ⁿ

Upvote

Similar Questions for you

If ²⁰C_r is the co-efficient of x^r in the expansion of (1 + x)²⁰, then the value of $\sum_{r = 0}^{20} r^{2}$ ²⁰C_r is equal to

Vishal Baghel

Kindly consider the following figure

If the coefficient of x¹⁰ in the binomial expansion of ${(\frac{\sqrt[]{x}}{5^{\frac{1}{4}}} + \frac{\sqrt[]{5}}{x^{\frac{1}{3}}})}^{60}$ is $5^{k} . l,$ where $l, k \in N a n d l$  is co-prime to 5, then k is equal to………...

Alok Kumar Singh

$T_{r + 1} =^{60} C_{r} {(x^{\frac{1}{2}})}^{60 - r} {(x^{- \frac{1}{3}})}^{r} {(5^{\frac{- 1}{4}})}^{60 - r} {(5^{\frac{1}{2}})}^{r}$

for

$x^{10} \frac{60 - r}{2} - \frac{r}{3} = 10$

$\Rightarrow 180 - 3 r - 2 r = 60$

->r = 24

k = 3 + exponent of 5 in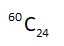

= $3 + ([\frac{60}{5}] + [\frac{60}{5^{2}}] - [\frac{24}{5}] - [\frac{24}{5^{2}}] - [\frac{36}{5}] - [\frac{36}{5^{2}}])$

= 3 + (12 + 2 – 4 – 0 – 7 – 1)

= 3 + 2 = 5

Payal Gupta

15. ${[3 x^{2} - 2 a x + 3 a^{2}]}^{3}$

= ${[3 x^{2} + a (- 2 x + 3 a)]}^{3}$

We know that by binomial theorem,

${(a + b)}^{3}$ = $a^{3} + b^{3} + 3 a b (a + b)$

= $a^{3} + b^{3} + 3 a^{2} b + 3 a b^{2}$

Then,

${[3 x^{2} + a (- 2 x + 3 a)]}^{3}$

= (3x²)³ + ${[a (- 2 x + 3 a)]}^{3}$ + $[3 (3 x^{2})^{2} a (- 2 x + 3 a)]$ + $[3 (3 x^{2}) {a (- 2 x + 3 a)}^{2}]$

= 27x⁶ + $[a^{3} {(- 2 x + 3 a)}^{3}]$ + $[3 (9 x^{4}) (- 2 a x + 3 a^{2})]$ + $[3 (3 x^{2}) {a^{2} {(3 a - 2 x)}^{2}}]$

= 27x⁶ + $[a^{3} {- 8 x^{3} + 27 a^{3} + 3 (4 x^{2}) (3 a) + 3 (- 2 x) (9 a^{2})}]$ + $[- 54 a x^{5} + 81 a^{2} x^{4}]$ + [ $(9 a^{2} x^{2})$ $(9 a^{2} + 4 x^{2} - 12 a x)$ ]

= 27x⁶ + [ $- 8 a^{3} x^{3} + 27 a^{6} + 36 a^{4} x^{2} - 54 a^{5} x$ ] + [ $- 54 a x^{5} + 81 a^{2} x^{4}$ ] + [ $(81 a^{4} x^{2} + 36 a^{2} x^{4} - 108 a^{3} x^{3}$ ]

= 27x⁶ $- 8 a^{3} x^{3} + 27 a^{6} + 36 a^{4} x^{2} - 54 a^{5} x$ $- 54 a x^{5} + 81 a^{2} x^{4}$ + $81 a^{4} x^{2} + 36 a^{2} x^{4} - 108 a^{3} x^{3}$

= 27x⁶– 54ax⁵ $+ 117 a^{2} x^{4}$ $- 116 a^{3} x^{3}$

Payal Gupta

15. ${[3 x^{2} - 2 a x + 3 a^{2}]}^{3}$

= ${[3 x^{2} + a (- 2 x + 3 a)]}^{3}$

We know that by binomial theorem,

${(a + b)}^{3}$ = $a^{3} + b^{3} + 3 a b (a + b)$

= $a^{3} + b^{3} + 3 a^{2} b + 3 a b^{2}$

Then,

${[3 x^{2} + a (- 2 x + 3 a)]}^{3}$

= (3x²)³ + ${[a (- 2 x + 3 a)]}^{3}$ + $[3 (3 x^{2})^{2} a (- 2 x + 3 a)]$ + $[3 (3 x^{2}) {a (- 2 x + 3 a)}^{2}]$

= 27x⁶ + $[a^{3} {(- 2 x + 3 a)}^{3}]$ + $[3 (9 x^{4}) (- 2 a x + 3 a^{2})]$ + $[3 (3 x^{2}) {a^{2} {(3 a - 2 x)}^{2}}]$

= 27x⁶ + $[a^{3} {- 8 x^{3} + 27 a^{3} + 3 (4 x^{2}) (3 a) + 3 (- 2 x) (9 a^{2})}]$ + $[- 54 a x^{5} + 81 a^{2} x^{4}]$ + [ $(9 a^{2} x^{2})$ $(9 a^{2} + 4 x^{2} - 12 a x)$ ]

= 27x⁶ + [ $- 8 a^{3} x^{3} + 27 a^{6} + 36 a^{4} x^{2} - 54 a^{5} x$ ] + [ $- 54 a x^{5} + 81 a^{2} x^{4}$ ] + [ $(81 a^{4} x^{2} + 36 a^{2} x^{4} - 108 a^{3} x^{3}$ ]

= 27x⁶ $- 8 a^{3} x^{3} + 27 a^{6} + 36 a^{4} x^{2} - 54 a^{5} x$ $- 54 a x^{5} + 81 a^{2} x^{4}$ + $81 a^{4} x^{2} + 36 a^{2} x^{4} - 108 a^{3} x^{3}$

= 27x⁶– 54ax⁵ $+ 117 a^{2} x^{4}$ $- 116 a^{3} x^{3}$

Payal Gupta

13. The general term of the expansion ${(3 + a x)}^{9}$ is

T_r₊₁ = ⁹C_r $3^{(9 - r)}$ ${(a x)}^{r}$

= ⁹C_r $3^{(9 - r)} a^{r} x^{r}$

At r = 2,

T₂₊₁ = ⁹C₂ $3^{(9 - 2)} a^{2} x^{2}$

= $\frac{9!}{2! (9 - 2)!}$ 3⁷a²x²

= $9′$ $8′$ $7!$ / $2′$ $1′$ $7!$ 3⁷a²x²

= 36 ×3⁷a²x²

At r = 3,

T₃₊₁ = ⁹C₃ $3^{(9 - 3)} a^{3} x^{3}$

= $\frac{9!}{3! (9 - 3)!}$ 3⁶a³x³

= 9'8'7'6!/3'2'1'6! 3⁶a³x³

= 84 ×3⁶a³x³

Given that,

Co-efficient of $x^{2}$ = co-efficient of $x^{3}$

=> 36 × $3^{7} a^{2}$ = 84 ×

Taking an Exam? Selecting a College?

Get authentic answers from experts, students and alumni that you won't find anywhere else.

On Shiksha, get access to

66K

Colleges

1.2K

Exams

6.9L

Reviews

1.8M

Answers

Learn more about...

Maths Ncert Solutions class 11th 2026

View Exam Details

82 Answered Questions

Share Your College Life Experience

Didn't find the answer you were looking for?

Search from Shiksha's 1 lakh+ Topics

Ask Current Students, Alumni & our Experts

Quick Actions

Community GuidelinesUser Points System

QuestionsDiscussionsTags

Have a question related to your career & education?

See what others like you are asking & answering