25. An analysis of monthly wages paid to workers in two firms A and B, belonging to the same industry, gives the following results:
Firm A Firm B
No. of wage earners 586 648
Mean of monthly wages ? 5253 ?5253
Variance of the distribution 100 121
of wages
(i) Which firm A or B pays larger amount as monthly wages?
(ii) Which firm, A or B, shows greater variability in individual wages?
25. An analysis of monthly wages paid to workers in two firms A and B, belonging to the same industry, gives the following results:
Firm A Firm B
No. of wage earners 586 648
Mean of monthly wages ? 5253 ?5253
Variance of the distribution 100 121
of wages
(i) Which firm A or B pays larger amount as monthly wages?
(ii) Which firm, A or B, shows greater variability in individual wages?
(i) The number of wage earner in firm A, nA=586. Mean monthly wages of firm
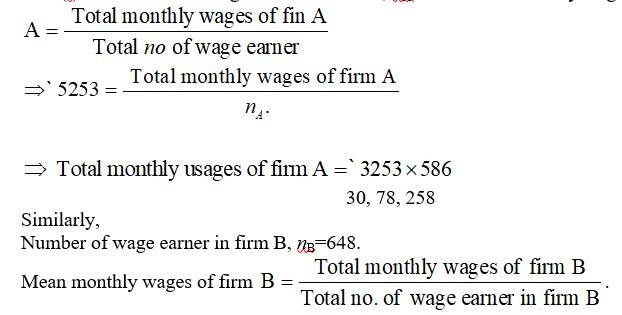
Total no of were canner in firm B.
Total monthly mages in firm. B = ?5253 * nB
=? 5253 * 586
=? 34, 03, 944
Firm B pays larger amount of monthly wages.
(ii) Since both the firm A and B has same mean monthly wages the firm wi
Similar Questions for you
Variance =
α2 + β2 = 897.7 × 8
= 7181.6
xi | fi | c.f. |
0 – 4 4 – 8 8 – 12 12 – 16 16 – 20 | 2 4 7 8 6 | 2 6 13 21 27 |
So, we have median lies in the class 12 – 16
I1 = 12, f = 8, h = 4, c.f. = 13
So, here we apply formula
20 M = 20 × 12.25
= 245
212 + a + b = 330
⇒ a + b = 118
= 3219
11760 + a2 + b2 = 19314
⇒ a2 + b2 = 19314 – 11760
= 7554
(a + b)2 –2ab = 7554
From here b = 41.795
a + b = 118
⇒ a + b + 2b = 118 + 83.59
= 201.59
Kindly go throuigh the solution
Given
&
(i) & (ii)
Now variance = 1 given
->(a - b) (a - b + 4) = 0
Since
Variance =
Let 2a2 – a + 1 = 5x
D = 1 – 4 (2) (1 – 5n)
= 40n – 7, which is not
As each square form is
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else.
On Shiksha, get access to
Learn more about...

Maths Ncert Solutions class 11th 2026
View Exam DetailsMost viewed information
SummaryDidn't find the answer you were looking for?
Search from Shiksha's 1 lakh+ Topics
Ask Current Students, Alumni & our Experts
Have a question related to your career & education?
See what others like you are asking & answering
