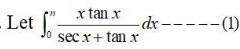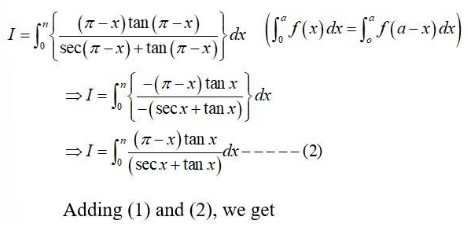259 ∫0nxtanxsecx+tanxdx

2I=∫0nπtanxsecx+tanxdx⇒2I=π∫0nsinxcosx1cosx+sinxcosxdx⇒2I=π∫0πsinx+1−11+sinxdx⇒2I=π∫0π1.dx−π∫0π11+sinxdx⇒2I=π∫0π1.dx−π∫0π(1−sinx)(1+sinx)(1−sinx)dx ⇒2I=π[x]0π−π∫0π1−sinxcos2xdx⇒2I=π2−π∫0π(sec2x−tanxsecx)dx⇒2I=π2−π[tanx−secx]0π ⇒2I=π2−π[tanπ−secπ−tan0+sec0]⇒2I=π2−π[0−(−1)−0+1]⇒2I=π2−2π⇒2I=π(π−2)I=π2(π−2)

259 $\int_{0}^{n} \frac{x t a n x}{s e c x + t a n x} d x$

2 Views|Posted 7 months ago

Asked by Shiksha User

1 Answer

Sort by:

Answered by

Vishal Baghel | Contributor-Level 10

7 months ago

$\begin{array}{l} 2 I = \int_{0}^{n} \frac{π t a n x}{s e c x + t a n x} d x \Rightarrow 2 I = π \int_{0}^{n} \frac{\frac{s i n x}{c o s x}}{\frac{1}{c o s x} + \frac{s i n x}{c o s x}} d x \\ \Rightarrow 2 I = π \int_{0}^{π} \frac{s i n x + 1 - 1}{1 + s i n x} d x \\ \Rightarrow 2 I = π \int_{0}^{π} 1 . d x - π \int_{0}^{π} \frac{1}{1 + s i n x} d x \\ \Rightarrow 2 I = π \int_{0}^{π} 1 . d x - π \int_{0}^{π} \frac{(1 - s i n x)}{(1 + s i n x) (1 - s i n x)} d x \end{array}$

$\begin{array}{l} \Rightarrow 2 I = π {[x]}_{0}^{π} - π \int_{0}^{π} \frac{1 - s i n x}{c o s^{2} x} d x \\ \Rightarrow 2 I = π^{2} - π \int_{0}^{π} (s e c^{2} x - t a n x s e c x) d x \\ \Rightarrow 2 I = π^{2} - π {[t a n x - s e c x]}_{0}^{π} \end{array}$

$\begin{array}{l} \Rightarrow 2 I = π^{2} - π [t a n π - s e c π - t a n 0 + s e c 0] \\ \Rightarrow 2 I = π^{2} - π [0 - (- 1) - 0 + 1] \\ \Rightarrow 2 I = π^{2} - 2 π \\ \Rightarrow 2 I = π (π - 2) \\ I = \frac{π}{2} (π - 2) \end{array}$

Upvote

Similar Questions for you

The value of $\int_{0}^{π / 4} \frac{x d x}{s i n^{4} (2 x) + c o s^{4} (2 x)}$  equal to

Alok Kumar Singh

$I = \int_{0}^{π / 4} \frac{x d x}{s i n^{4} (2 x) + c o s^{4} (2 x)}$

Let 2x = t then $d x = \frac{1}{2} d t$

$I = \int_{}^{} \frac{\frac{t}{2} \cdot \frac{1}{2} d t}{s i n^{4} t + c o s^{4} t}$

$= \frac{1}{4} \int_{0}^{π / 2} \frac{t d t}{s i n^{4} t + c o s^{4} t} d t$

$I = \frac{1}{4} \int_{0}^{π / 2} \frac{(\frac{π}{2} - t) d t}{s i n^{4} t + c o s^{4} t} d t$

$2 I = \frac{1}{4} \int_{0}^{π / 2} \frac{\frac{π}{2} d t}{s i n^{4} t + c o s^{4} t}$

$2 I = \frac{π}{8} \int_{0}^{π / 2} \frac{s i n^{4} t d t}{t a n^{4} t + 1}$

Let tan t = y then

$2 I = \frac{π}{8} \int_{0}^{\infty} \frac{(1 + y^{2}) d y}{1 + y^{4}}$

$= \frac{π}{8} \int_{0}^{\infty} \frac{1 + \frac{1}{y^{2}}}{y^{2} + \frac{1}{y^{2}} - 2 + 2} d y$

$= \frac{π}{8} \int_{0}^{\infty} \frac{(1 + \frac{1}{y^{2}}) d y}{2 + {(y - \frac{1}{y})}^{2}}$

Let

Alok Kumar Singh

$k = \frac{[\vec{a} \vec{b} \vec{c}] + 2 [\vec{a} \vec{b} \vec{c}] + [\vec{a} \vec{b} \vec{c}] - [\vec{a} \vec{b} \vec{c}]}{[\vec{a} \vec{b} \vec{c}]}$

k = 3

Alok Kumar Singh

$\underset{x \to 0}{l i m} {[s i n^{2} (\frac{π}{2 - 3 x})]}^{s e c^{2} (\frac{π}{2 - 5 x})}$

$e^{\underset{x \to 0}{l i m} [s i n^{2} (\frac{π}{2 - 3 x}) - 1] s e c^{2} (\frac{π}{2 - 5 x})}$

$= e^{\underset{x \to 0}{l i m} \frac{- s i n^{2} (\frac{- 3 π x}{2 (2 - 3 x)})}{s i n^{2} (\frac{- 5 π x}{2 (2 - 5 x)})}} = e^{- \frac{9}{25}}$

For real numbers α, β, γ and δ, if ∫ [ (x²-1) + tan⁻¹((x²+1)/x) ] / [ (x⁴+3x²+1)tan⁻¹((x²-1)/x) ] dx = αlogₑ|tan⁻¹((x²+1)/x)| + βtan⁻¹((γ(x²-1))/x) + δtan⁻¹((x²+1)/x) + C where C is an arbitrary constant, then the value of 10(α + βγ + δ) is equal to........

Alok Kumar Singh

The integral is I = ∫ [ (x²-1) + tan? ¹ (x + 1/x)] / [ (x? +3x²+1)tan? ¹ (x+1/x)] dx
This is a complex integral. The provided solution splits it into two parts:
I? = ∫ (x²-1) / [ (x? +3x²+1)tan? ¹ (x+1/x)] dx
I? = ∫ 1 / (x? +3x²+1) dx
The solution proceeds with substitutions which are hard to follow due

Kindly considwer the following

Alok Kumar Singh

The problem is to evaluate the integral:
I = ∫? ¹? [x] * e^ [x] / e^ (x-1) dx, where [x] denotes the greatest integer function.

The solution breaks the integral into a sum of integrals over unit intervals:
I = ∑? ∫? ¹ n * e? / e^ (x-1) dx
= ∑? n * e? ∫? ¹ e^ (1-x) dx
= ∑? n * e? [-e^ (1-x)] from n to n+1