Ask & Answer Question

Relations and Functions Ncert Solutions Maths class 12th Maths Class 12th Relations and Functions

57. Let f: W → W be defined as f(n) = n − 1, if is odd and f(n) = n + 1, if n is even. Show that f is invertible. Find the inverse of f. Here, W is the set of all whole numbers.

26 Views | Posted 4 months ago

Asked by Shiksha User

1 Answer

Answered by

Vishal Baghel | Contributor-Level 10

4 months ago

It is given that:

$f : W \to W$ is defined as $f (n) = {\begin{cases} n - 1, i f . n, o d d \\ n + 1, i f . n, e v e n \end{cases}$

One-one:

Let, $f (n) = f (m) .$

It can be observed that if n is odd and m is even, then we will have n-1=m+1.

$\Rightarrow n - m = 2$

However, the possibility of n being even and m being odd can also be ignored under a similar argument.

$∴$ Both n and m must be either odd or even.

Now, if both n and m are odd, then we have:

$f (n) = f (m) \Rightarrow n - 1 = m - 1 \Rightarrow n = m$

Again, if both n and m are even, then we have:

$f (n) = f (m) \Rightarrow n + 1 = m + 1 \Rightarrow n = m$

$∴ f$ is one-one.

It is clear that any odd number 2r+1 in co-domain N is the image of 2r in domain N and any even 2r in co-domain N is the image of 2r+1 in domain N.

$∴ f$ is onto.

Hence, f is an invertible function.

Let us define $g : W \to W$ as:

$g (m) = {\begin{cases} m + 1, i f . n, e v e n \\ m - 1, i f . n, o d d \end{cases}$

Now, when n is odd:

$g o f (n) = g (f (n)) = g (n - 1) = n - 1 + 1 = n$

And, when

...more

It is given that:

$f : W \to W$ is defined as $f (n) = {\begin{cases} n - 1, i f . n, o d d \\ n + 1, i f . n, e v e n \end{cases}$

One-one:

Let, $f (n) = f (m) .$

It can be observed that if n is odd and m is even, then we will have n-1=m+1.

$\Rightarrow n - m = 2$

However, the possibility of n being even and m being odd can also be ignored under a similar argument.

$∴$ Both n and m must be either odd or even.

Now, if both n and m are odd, then we have:

$f (n) = f (m) \Rightarrow n - 1 = m - 1 \Rightarrow n = m$

Again, if both n and m are even, then we have:

$f (n) = f (m) \Rightarrow n + 1 = m + 1 \Rightarrow n = m$

$∴ f$ is one-one.

It is clear that any odd number 2r+1 in co-domain N is the image of 2r in domain N and any even 2r in co-domain N is the image of 2r+1 in domain N.

$∴ f$ is onto.

Hence, f is an invertible function.

Let us define $g : W \to W$ as:

$g (m) = {\begin{cases} m + 1, i f . n, e v e n \\ m - 1, i f . n, o d d \end{cases}$

Now, when n is odd:

$g o f (n) = g (f (n)) = g (n - 1) = n - 1 + 1 = n$

And, when n is even:

$g o f (n) = g (f (n)) = g (n + 1) = n + 1 - 1 = n$

Similarly, when m is odd:

$f o g (m) = f (g (m)) = f (m - 1) = m - 1 + 1 = m$

When m is even:

$\begin{array}{l} f o g (m) = f (g (m)) = f (m + 1) = m + 1 - 1 = m \\ ∴ g o f = I_{W}, a n d, f o g = I_{W} \end{array}$

Thus, f is invertible and the inverse of f is given by $f^{- 1} = g$ , which is the same as f.

Hence, the inverse of f is f itself.

less

0 Upvotes 0 Downvotes

Similar Questions for you

Let S = {1, 2, 3 ,....,20}

R₁ = {(a, b) : a divide b}

R₂ = {(a, b) : a is integral multiple of b} a, b Î s

n(R₁ – R₂) = ?

alok kumar singh

R₁ = { (1, 1) (1, 2), (1, 3)., (1, 20), (2, 2), (2, 4). (2, 20), (3, 3), (3, 6), . (3, 18),
(4, 4), (4, 8), . (4, 20), (5, 5), (5, 10), (5, 15), (5, 20), (6, 6), (6, 12), (6, 18), (7. 7),
(7, 14), (8, 8), (8, 16), (9, 9), (9, 18), (10, 10), (10, 20), (11, 11), (12, 12), . (20, 20)}

n (R₁) = 66

R₂ = {a is integral multiple of b}

So n (R₁ – R₂) = 66 – 20 = 46

as R₁ Ç R₂ = { (a, a) : a Î s} = { (1, 1), (2, 2), ., (20, 20)}

$f (x) = {\begin{matrix} e^{- x}, & x < 0 \\ l n x, & x > 0 \end{matrix}$

$g (x) = {\begin{matrix} e^{x}, & x < 0 \\ x, & x > 0 \end{matrix}$

The gof : A->R is

alok kumar singh

$g o f (x) = {\begin{matrix} f (x), & f (x) < 0 \\ f (x), & f (x) > 0 \end{matrix}$

$= {\begin{array}{l} e^{l n x} = x & (0, 1) & e^{- x} \\ (- \infty, 0) & l n x & (1, \infty) \end{array}$

If A = {1, 2, 3, … 100}, R = {(x, y) | 2x = 3y, x, y ∈ A} is symmetric relation on A and the number of elements in R is n, the smallest integer value of n is

alok kumar singh

$?$ R is symmetric relation

⇒ (y, x) ∈ R V (x, y) ∈ R

(x, y) ∈ R ⇒ 2x = 3y and (y, x) ∈ R ⇒ 3x = 2y

Which holds only for (0, 0)

Which does not belongs to R.

∴ Value of n = 0

Let : f(0, R)->∞ be increasing function such that $\underset{x \to \infty}{l i m} \frac{f (7 x)}{f (x)} = 1$ then $\underset{x \to \infty}{l i m} (\frac{f (5 x)}{f (x)} - 1)$ is equal to

alok kumar singh

f is increasing function

x < 5x < 7x

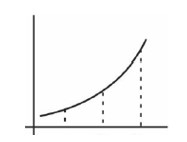
f (x) < f (5x) < f (7x)

$\frac{f (x)}{f (x)} < \frac{f (5 x)}{f (x)} < \frac{f (7 x)}{f (x)}$

$\underset{x \to \infty}{l i m} \frac{f (x)}{f (x)} < \underset{x \to \infty}{l i m} \frac{f (5 x)}{f (x)} < \underset{x \to \infty}{l i m} \frac{f (7 x)}{f (x)}$

-> $1 < \underset{x \to \infty}{l i m} \frac{f (5 x)}{f (x)} < 1$ $\underset{x \to \infty}{l i m} \frac{f (5 x)}{f (x)} = 1$

$\underset{x \to \infty}{l i m} (\frac{f (5 x)}{f (x)} - 1) = 0$

Let A = ${1, 2, 3, . . . . ., 10} a n d f : A \to A$ be defined as

$f (k) = {\begin{matrix} k + 1 & i f k i s o d d \\ k & i f k i s e v e n \end{matrix}$

Then the number of possible functions g : A ® A such that gof = f is:

alok kumar singh

Given f (k) = ${\begin{cases} k + 1, k i s o d d \\ k, k i s e v e n \end{cases}$

$? g : A \to A$ such that g (f (x) = f (x)

Case I : If x is even then g (x) = x . (i)

Case II : If x is odd then g (x + 1) = x + 1 . (ii)

From (i) & (ii), g (x) = x, when x is even

So total no. of functions = 10⁵ × 1 = 10⁵

Get authentic answers from experts, students and alumni that you won't find anywhere else

On Shiksha, get access to

65k Colleges
1.2k Exams
687k Reviews
1800k Answers

Community GuidelinesUser Points System

QuestionsDiscussionsTags

57. Let f: W → W be defined as f(n) = n − 1, if is odd and f(n) = n + 1, if n is even. Show that f is invertible. Find the inverse of f. Here, W is the set of all whole numbers.

1 Answer

Similar Questions for you

Learn more about...

Most viewed information

Most viewed information

Share Your College Life Experience

Didn't find the answer you were looking for?

Need guidance on career and education? Ask our experts

Your Question