A committee of 6 is to be chosen from 10 men and 7 women so as to contain at least 3 men and 2 women. In how many different ways can this be done if two particular women refuse to serve on the same committee?
[Hint: At least 3 men and 2 women: The number of ways = 10C3 * 10C3 + 10C4 * 7C2. For 2 particular women to be always there: the number of ways = 10C4 * 10C3 * 5C1. The total number of committees when two particular women are never together = Total – together.]
A committee of 6 is to be chosen from 10 men and 7 women so as to contain at least 3 men and 2 women. In how many different ways can this be done if two particular women refuse to serve on the same committee?
[Hint: At least 3 men and 2 women: The number of ways = 10C3 * 10C3 + 10C4 * 7C2. For 2 particular women to be always there: the number of ways = 10C4 * 10C3 * 5C1. The total number of committees when two particular women are never together = Total – together.]
This is a Fill in the blanks Type Questions as classified in NCERT Exemplar
Similar Questions for you
...(1)
–2α + β = 0 …(2)
Solving (1) and (2)
a =
Variance =
α2 + β2 = 897.7 × 8
= 7181.6
Start with
(1)
(2)
(3) GTE : 4!, GTN: 4!, GTT : 4!
(4) GTWENTY = 1
⇒ 360 + 60 + 60 + 24 + 24 + 24 + 1 = 553
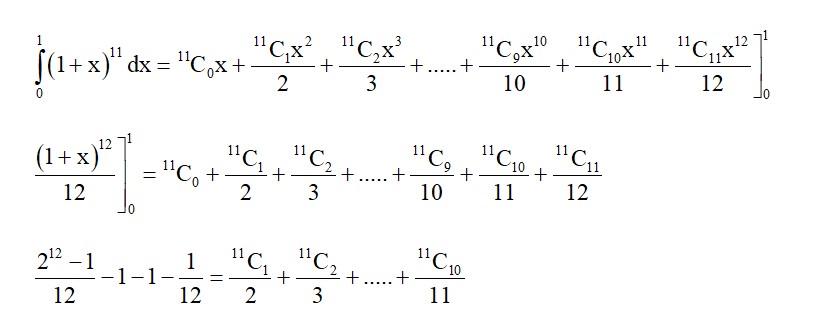
->g(x) = |x|, x Î (–3, 1)
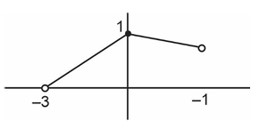
Range of fog(x) is [0, 1]
Range of fog(x) is [0, 1]
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else.
On Shiksha, get access to
Learn more about...

Maths NCERT Exemplar Solutions Class 11th Chapter Seven 2025
View Exam DetailsMost viewed information
SummaryDidn't find the answer you were looking for?
Search from Shiksha's 1 lakh+ Topics
Ask Current Students, Alumni & our Experts
Have a question related to your career & education?
See what others like you are asking & answering