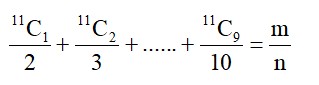Consider the following frequency distribution:
| Class: | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 |
|---|---|---|---|---|---|
| Frequency: | α | 110 | 54 | 30 | β |
If the sum of all frequencies is 584 and median is 45, then |α - β| is equal to…….
Consider the following frequency distribution:
| Class: | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 |
|---|---|---|---|---|---|
| Frequency: | α | 110 | 54 | 30 | β |
If the sum of all frequencies is 584 and median is 45, then |α - β| is equal to…….
α+110+54+30+β=584 ⇒ α+β=390.
Median=45. L=40, N=584, C=α+110+54=α+164, f=30, h=10.
45 = 40 + [ (292- (α+164)/30]*10 = 40 + (128-α)/3.
5 = (128-α)/3 ⇒ 15=128-α ⇒ α=113.
β = 390-113=277.
|α-β|=164.
Similar Questions for you
...(1)
–2α + β = 0 …(2)
Solving (1) and (2)
a =
Variance =
α2 + β2 = 897.7 × 8
= 7181.6
Start with
(1)
(2)
(3) GTE : 4!, GTN: 4!, GTT : 4!
(4) GTWENTY = 1
⇒ 360 + 60 + 60 + 24 + 24 + 24 + 1 = 553
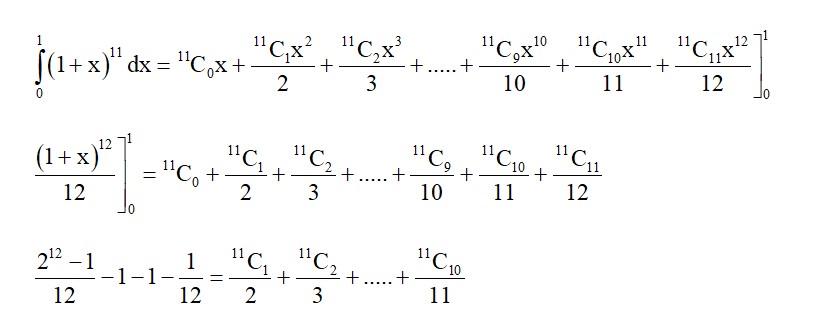
->g(x) = |x|, x Î (–3, 1)
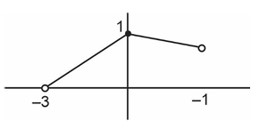
Range of fog(x) is [0, 1]
Range of fog(x) is [0, 1]
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else.
On Shiksha, get access to
Didn't find the answer you were looking for?
Search from Shiksha's 1 lakh+ Topics
Ask Current Students, Alumni & our Experts
Have a question related to your career & education?
See what others like you are asking & answering