Identify the quantifiers in the following statements:
i. There exists a triangle that is not equilateral.
ii. For all real numbers and , .
iii. There exists a real number that is not a rational number.
iv. For every natural number , is also a natural number.
v. For all real numbers with , .
vi. There exists a triangle that is not an isosceles triangle.
vii. For all negative integers , is also a negative integer.
viii. There exists a statement in the above statements that is not true.
ix. There exists an even prime number other than 2.
x. There exists a real number such that .
Identify the quantifiers in the following statements:
i. There exists a triangle that is not equilateral.
ii. For all real numbers and , .
iii. There exists a real number that is not a rational number.
iv. For every natural number , is also a natural number.
v. For all real numbers with , .
vi. There exists a triangle that is not an isosceles triangle.
vii. For all negative integers , is also a negative integer.
viii. There exists a statement in the above statements that is not true.
ix. There exists an even prime number other than 2.
x. There exists a real number such that .
-
1 Answer
-
This is a short answer type question as classified in NCERT Exemplar
Similar Questions for you
Case – I
it can be false if r is false,
so not a tautology
Case – II If
tautology
then
Case – I
pva
its negation as asked in question
=
=
mod (7)
…… (i)
Now,
……. (ii)
(i) & (ii)
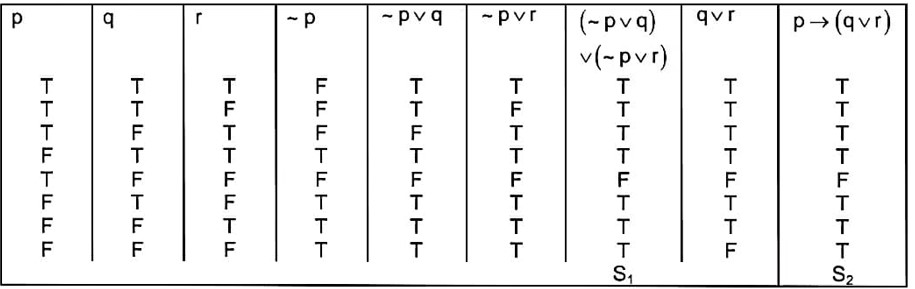
kindly consider the following Image
q is equivalent to
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 65k Colleges
- 1.2k Exams
- 687k Reviews
- 1800k Answers