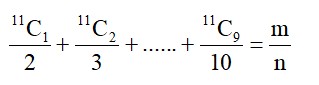Let A, B, C be three points whose position vectors respectively are
If a is the smallest positive integer for which are noncollinear, then the length of the median, in through A is:
Let A, B, C be three points whose position vectors respectively are
If a is the smallest positive integer for which are noncollinear, then the length of the median, in through A is:
Mid point of BC is
For = 1, and will be collinear. So for non collinearity
= 2
Similar Questions for you
...(1)
–2α + β = 0 …(2)
Solving (1) and (2)
a =
Variance =
α2 + β2 = 897.7 × 8
= 7181.6
Start with
(1)
(2)
(3) GTE : 4!, GTN: 4!, GTT : 4!
(4) GTWENTY = 1
⇒ 360 + 60 + 60 + 24 + 24 + 24 + 1 = 553
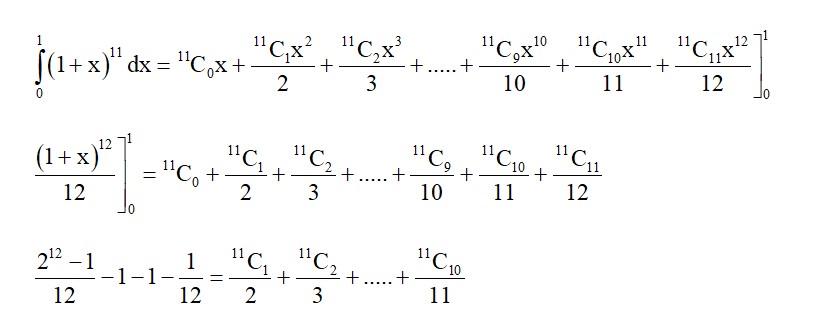
->g(x) = |x|, x Î (–3, 1)
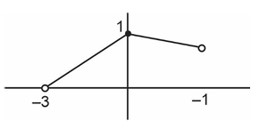
Range of fog(x) is [0, 1]
Range of fog(x) is [0, 1]
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else.
On Shiksha, get access to
Learn more about...
Didn't find the answer you were looking for?
Search from Shiksha's 1 lakh+ Topics
Ask Current Students, Alumni & our Experts
Have a question related to your career & education?
See what others like you are asking & answering