Relations and Functions Ncert Solutions Maths class 12th Maths Class 12th Relations and Functions

Relation and Function Exercise 1.2 Solutions

17. Show that the function f: R* → R* defined by f(x) = 1/x is one-one and onto, where: R* is the set of all non-zero real numbers. Is the result true, if the domain: R* is replaced by N with the co-domain being same as: R*?

3 Views | Posted 4 months ago

1 Answer

Answered by

Vishal Baghel | Contributor-Level 10

4 months ago

The $f x$ n is $f (x) = \frac{1}{x}$ , which is a $f : R_{*}$ $\to$ $R_{*}$ and $R_{*}$ is set of all non-zero real numbers

For, $x_{1}, x_{2} \in R_{*}, f (x_{1}) = f (x_{2})$

$\Rightarrow \frac{1}{x_{1}} = \frac{1}{x_{2}}$

$\Rightarrow x_{1} = x_{2}$ So, $f$ is one-one

For, $y \in R_{*},$ $x = \frac{1}{f (x)} = \frac{1}{y}$ such that

So, $f (x) = y$

So, every element in the co-domain has a pre-image in $f$

So, $f$ is onto

If $f : N \to R_{*}$ such that $f (x) = \frac{1}{x}$

For, $x_{1}, x_{2} \in N,$ $f (x_{1}) = f (x_{2})$

$\Rightarrow \frac{1}{x_{1}} = \frac{1}{x_{2}}$

$\Rightarrow x_{1} = x_{2}$ So, $f$ is one-one

For, $y \in R_{*}$ and $f (x) = y$ we have $x = \frac{1}{y} \notin N$

Eg., $3 \in R_{*}$ so $x = \frac{1}{3} \notin N$

So, $f$ is not onto

0 Upvotes 0 Downvotes

Similar Questions for you

Let S = {1, 2, 3 ,....,20}

R₁ = {(a, b) : a divide b}

R₂ = {(a, b) : a is integral multiple of b} a, b Î s

n(R₁ – R₂) = ?

alok kumar singh

R₁ = { (1, 1) (1, 2), (1, 3)., (1, 20), (2, 2), (2, 4). (2, 20), (3, 3), (3, 6), . (3, 18),
(4, 4), (4, 8), . (4, 20), (5, 5), (5, 10), (5, 15), (5, 20), (6, 6), (6, 12), (6, 18), (7. 7),
(7, 14), (8, 8), (8, 16), (9, 9), (9, 18), (10, 10), (10, 20), (11, 11), (12, 12), . (20, 20)}

n (R₁) = 66

R₂ = {a is integral multiple of b}

So n (R₁ – R₂) = 66 – 20 = 46

as R₁ Ç R₂ = { (a, a) : a Î s} = { (1, 1), (2, 2), ., (20, 20)}

$f (x) = {\begin{matrix} e^{- x}, & x < 0 \\ l n x, & x > 0 \end{matrix}$

$g (x) = {\begin{matrix} e^{x}, & x < 0 \\ x, & x > 0 \end{matrix}$

The gof : A->R is

alok kumar singh

$g o f (x) = {\begin{matrix} f (x), & f (x) < 0 \\ f (x), & f (x) > 0 \end{matrix}$

$= {\begin{array}{l} e^{l n x} = x & (0, 1) & e^{- x} \\ (- \infty, 0) & l n x & (1, \infty) \end{array}$

If A = {1, 2, 3, … 100}, R = {(x, y) | 2x = 3y, x, y ∈ A} is symmetric relation on A and the number of elements in R is n, the smallest integer value of n is

alok kumar singh

$?$ R is symmetric relation

⇒ (y, x) ∈ R V (x, y) ∈ R

(x, y) ∈ R ⇒ 2x = 3y and (y, x) ∈ R ⇒ 3x = 2y

Which holds only for (0, 0)

Which does not belongs to R.

∴ Value of n = 0

Let : f(0, R)->∞ be increasing function such that $\underset{x \to \infty}{l i m} \frac{f (7 x)}{f (x)} = 1$ then $\underset{x \to \infty}{l i m} (\frac{f (5 x)}{f (x)} - 1)$ is equal to

alok kumar singh

f is increasing function

x < 5x < 7x

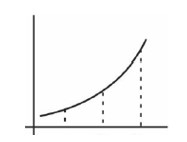
f (x) < f (5x) < f (7x)

$\frac{f (x)}{f (x)} < \frac{f (5 x)}{f (x)} < \frac{f (7 x)}{f (x)}$

$\underset{x \to \infty}{l i m} \frac{f (x)}{f (x)} < \underset{x \to \infty}{l i m} \frac{f (5 x)}{f (x)} < \underset{x \to \infty}{l i m} \frac{f (7 x)}{f (x)}$

-> $1 < \underset{x \to \infty}{l i m} \frac{f (5 x)}{f (x)} < 1$ $\underset{x \to \infty}{l i m} \frac{f (5 x)}{f (x)} = 1$

$\underset{x \to \infty}{l i m} (\frac{f (5 x)}{f (x)} - 1) = 0$

Let A = ${1, 2, 3, . . . . ., 10} a n d f : A \to A$ be defined as

$f (k) = {\begin{matrix} k + 1 & i f k i s o d d \\ k & i f k i s e v e n \end{matrix}$

Then the number of possible functions g : A ® A such that gof = f is:

alok kumar singh

Given f (k) = ${\begin{cases} k + 1, k i s o d d \\ k, k i s e v e n \end{cases}$

$? g : A \to A$ such that g (f (x) = f (x)

Case I : If x is even then g (x) = x . (i)

Case II : If x is odd then g (x + 1) = x + 1 . (ii)

From (i) & (ii), g (x) = x, when x is even

So total no. of functions = 10⁵ × 1 = 10⁵

Get authentic answers from experts, students and alumni that you won't find anywhere else

On Shiksha, get access to

65k Colleges
1.2k Exams
687k Reviews
1800k Answers

Community GuidelinesUser Points System

QuestionsDiscussionsTags

Relation and Function Exercise 1.2 Solutions

17. Show that the function f: R* → R* defined by f(x) = 1/x is one-one and onto, where: R* is the set of all non-zero real numbers. Is the result true, if the domain: R* is replaced by N with the co-domain being same as: R*?