The triangle of maximum area that can be inscribed in a given circle of radius 'r' is:

y (x) = ∫? (2t² - 15t + 10)dt
dy/dx = 2x² - 15x + 10.
For tangent at (a, b), slope is m = dx/dy = 1 / (dy/dx) = 1 / (2a² - 15a + 10).
Given slope is -1/3.
2a² - 15a + 10 = -3
2a² - 15a + 13 = 0 (The provided solution has 2a²-15a+7=0, suggesting a different problem or a typo)
Following the image: 2a² - 15a

f' (c) = 1 + lnc = e/ (e-1)
lnc = e/ (e-1) - 1 = (e - (e-1)/ (e-1) = 1/ (e-1)
c = e^ (1/ (e-1)

$CD=\sqrt[]{{\left(10+x^2\right)}^2-{\left(10-x^2\right)}^2}=2\sqrt[]{10}\left|x\right|$

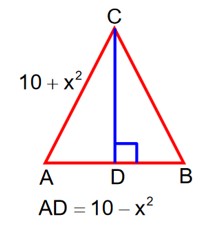
Area 

$=\frac{1}{2}\times CD\times AB=\frac{1}{2}\times 2\sqrt[]{10}\left|x\right|\left(20-2x^2\right)$

$\Rightarrow 10-x^2=2x$

3x² = 10

 x = k

3k² = 10

By truth table

So F₁ (A, B, C) is not a tautology

Now again by truth table

So      F₂ (A, B) be a tautology.

Given f(X) = ${\displaystyle {\int }_1^x\frac{lo{g}_{e}t}{\left(1+t\right)}dt............\left(i\right)}$  

So  $f\left(\frac{1}{x}\right)={\displaystyle {\int }_1^{1/x}\frac{\lambda lo{g}_{e}t}{1+t}dt}............\left(ii\right)$

put $t=\frac{1}{z}thendt=-\frac{1}{z^2}dz$

$f\left(\frac{1}{x}\right)={\displaystyle {\int }_1^x\frac{lo{g}_{e}t}{t\left(1+t\right)}}dt............\left(iii\right)$    

(i) + (iii), f(x) + $f\left(\frac{1}{x}\right)={\displaystyle {\int }_1^x\left(\frac{lo{g}_{e}t}{1+t}+\frac{lo{g}_{e}t}{t\left(1+t\right)}\right)dt}$

$={\left[\frac{{\left(lo{g}_{e}t\right)}^2}{2}\right]}_1^x=\frac{{\left(lo{g}_{x}x\right)}^2}{2}$  

Hence f(e) + $f\left(\frac{1}{e}\right)=\frac{1}{2}$