14.9 A spring having with a spring constant 1200 N m–1 is mounted on a horizontal table as shown in Fig. 14.24. A mass of 3 kg is attached to the free end of the spring. The mass is then pulled sideways to a distance of 2.0 cm and released.
Determine
(i) The frequency of oscillations
(ii) Maximum acceleration of the mass
(iii) The maximum speed of the mass
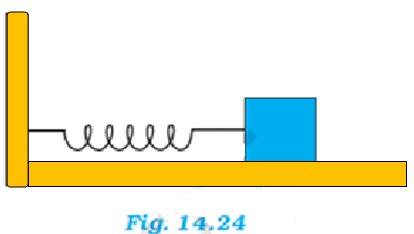
14.9 A spring having with a spring constant 1200 N m–1 is mounted on a horizontal table as shown in Fig. 14.24. A mass of 3 kg is attached to the free end of the spring. The mass is then pulled sideways to a distance of 2.0 cm and released.
Determine
(i) The frequency of oscillations
(ii) Maximum acceleration of the mass
(iii) The maximum speed of the mass

Spring constant, k = 1200 N/m
Mass, m = 3 kg
Displacement, d = 2 cm = 0.02 m
(a) Frequency of oscillation, v is given by
v = = = = 3.183 m/s
(b) Maximum acceleration (a) is given by the relation: a =
where, angular frequency = and A = maximum displacement
a = = = 8 m/
(c) Maximum velocity,
Similar Questions for you
Velocity of block in equilibrium, in first case,
Velocity of block in equilibrium, is second case,
From conservation of momentum,
Mv = (M + m) v’
f? = 300 Hz
3rd overtone = 7f? = 2100 Hz
Kindly consider the following figure
K = U
½ mω² (A² - x²) = ½ mω²x²
A² - x² = x²
A² = 2x²
x = ± A/√2
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else.
On Shiksha, get access to
Learn more about...

physics ncert solutions class 11th 2023
View Exam DetailsMost viewed information
SummaryDidn't find the answer you were looking for?
Search from Shiksha's 1 lakh+ Topics
Ask Current Students, Alumni & our Experts
Have a question related to your career & education?
See what others like you are asking & answering