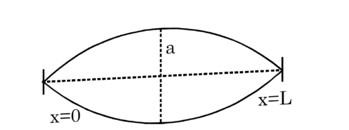
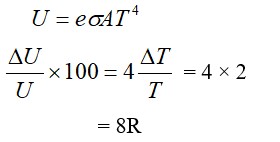A string of mass per unit length is clamped at both ends such that one end of the string is at x = 0 and the other end at x = L. When string vibrates in fundamental mode, amplitude of the midpoint of string is a and tension is string is F. Find the total oscillation energy (in J) stored in the string.
(Use L = 1m, F = 10 N, a =
A string of mass per unit length is clamped at both ends such that one end of the string is at x = 0 and the other end at x = L. When string vibrates in fundamental mode, amplitude of the midpoint of string is a and tension is string is F. Find the total oscillation energy (in J) stored in the string.
(Use L = 1m, F = 10 N, a =
4 Views|Posted 5 months ago
Asked by Shiksha User
1 Answer
Similar Questions for you
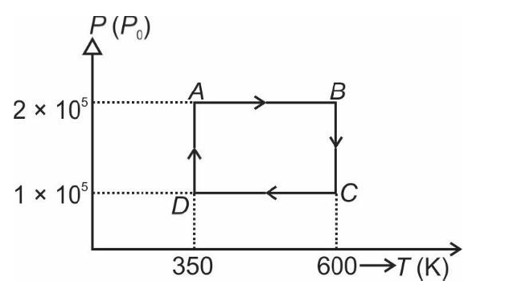
From A to B the process is isobaric
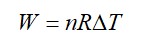
= W = 2 × R (600 - 350)
= 500 R
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else.
On Shiksha, get access to
66K
Colleges
|
1.2K
Exams
|
6.9L
Reviews
|
1.8M
Answers
Learn more about...

Physics Oscillations 2025
View Exam DetailsMost viewed information
SummaryDidn't find the answer you were looking for?
Search from Shiksha's 1 lakh+ Topics
or
Ask Current Students, Alumni & our Experts
Have a question related to your career & education?
or
See what others like you are asking & answering