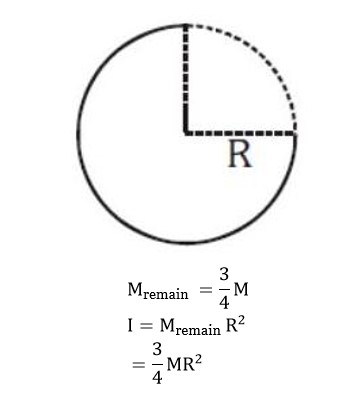
From a circular ring of mass ' M ' and radius ' R ' an arc corresponding to a 90° sector is removed. The moment of inertia of the remaining part of the ring about an axis passing through the centre of the ring and perpendicular to the plane of the ring is ' K ' times ' MR² '. Then the value of ' K ' is:
From a circular ring of mass ' M ' and radius ' R ' an arc corresponding to a 90° sector is removed. The moment of inertia of the remaining part of the ring about an axis passing through the centre of the ring and perpendicular to the plane of the ring is ' K ' times ' MR² '. Then the value of ' K ' is:
Option 1 - <p>3/4<br><!-- [if !supportLineBreakNewLine]--><br><!--[endif]--></p>
Option 2 - <p>7/8<br><!-- [if !supportLineBreakNewLine]--><br><!--[endif]--></p>
Option 3 - <p>1/4<br><!-- [if !supportLineBreakNewLine]--><br><!--[endif]--></p>
Option 4 - <p>1/8</p>
1 Views|Posted 5 months ago
Asked by Shiksha User
1 Answer
A
Answered by
5 months ago
Correct Option - 1
Detailed Solution:
Kindly go through the solution
Similar Questions for you
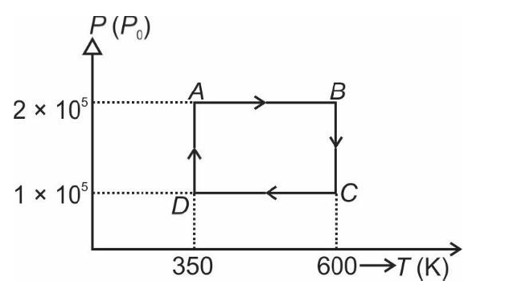
From A to B the process is isobaric
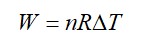
= W = 2 × R (600 - 350)
= 500 R
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else.
On Shiksha, get access to
66K
Colleges
|
1.2K
Exams
|
6.9L
Reviews
|
1.8M
Answers
Learn more about...

Physics System of Particles and Rotational Motion 2025
View Exam DetailsMost viewed information
SummaryDidn't find the answer you were looking for?
Search from Shiksha's 1 lakh+ Topics
or
Ask Current Students, Alumni & our Experts
Have a question related to your career & education?
or
See what others like you are asking & answering