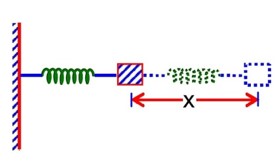
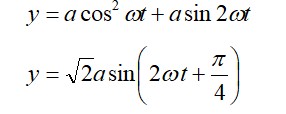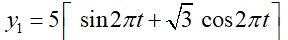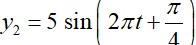The motion of a mass on a spring, with spring constant K is as shown in figure. The equation of motion is given by x(t) = 4 sin Suppose that at time t = 0, the position of mass is x(0) and velocity then its displacement can also be represented as x(t) = C cos where C and are:
The motion of a mass on a spring, with spring constant K is as shown in figure. The equation of motion is given by x(t) = 4 sin Suppose that at time t = 0, the position of mass is x(0) and velocity then its displacement can also be represented as x(t) = C cos where C and are:
x (t) = A sin t + B cos
At t = 0:
Similar Questions for you
Then,
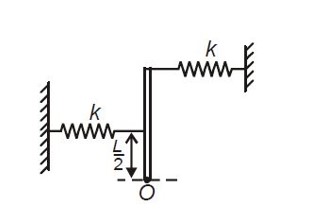
Given mg = kL
∴ Iα = (kLθ.L + k (L/2)²θ - mg (L/2)θ)
(mL²/3)α = kL² (3/4)θ (restoring torque)
α = (9k/4m)θ
∴ ω = (3/2)√ (k/m)
y = A sin (2πt/T)
t? - t? = (T/2π) [sin? ¹ (x? /A) - sin? ¹ (x? /A)]
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else.
On Shiksha, get access to
Learn more about...

Physics Oscillations 2025
View Exam DetailsMost viewed information
SummaryDidn't find the answer you were looking for?
Search from Shiksha's 1 lakh+ Topics
Ask Current Students, Alumni & our Experts
Have a question related to your career & education?
See what others like you are asking & answering