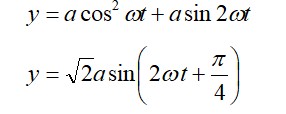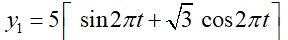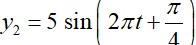Class 11th Physics Oscillations Physics Simple Harmonic Motion

Two particles A and B of equal masses are suspended from two massless springs of spring constants K₁ and K₂ respectively. If the maximum velocities during oscillations are equal, the ratio of the amplitude of A and B is

Option 1 - <p>√(K₁/K₂)<br><br></p>

Option 2 - <p>K₂/K₁<br><br></p>

Option 3 - <p>K₁/K₂<br><br></p>

Option 4 - <p>√(K₂/K₁)</p>

3 Views|Posted 5 months ago

Asked by Shiksha User

1 Answer

Sort by:

A

Answered by

Alok Kumar Singh | Contributor-Level 10

5 months ago

Correct Option - 2

Detailed Solution:

A? √* (K? /m)* = A? √* (K? /m)* ⇒ A? √K? = A? √K?

Upvote

Thumbs Down Icon

Similar Questions for you

The equation y = acos²ωt + asin²ωt is

Alok Kumar Singh

Two simple harmonic motion are represented by,

And



The ratio of their amplitudes is

$A_{1} = \sqrt[]{{(5)}^{2} + {(5 \sqrt[]{3})}^{2}} = 10$

$A_{2} = 5$

Then, $\frac{A_{1}}{A_{2}} = \frac{10}{5} = \frac{2}{1}$

For an SHM oscillator, the amplitude is 5 cm and its time period is 4 seconds. The minimum time taken by the particle to pass between points which are at distances 4 cm and 3 cm from the centre of oscillation on the same side of it will be

Alok Kumar Singh

$y = A \sin ? \frac{2 π t}{T}$

$t_{2} - t_{1} = \frac{T}{2 π} [\sin^{- 1} ? \frac{x_{1}}{A} - \sin^{- 1} ? \frac{x_{2}}{A}]$

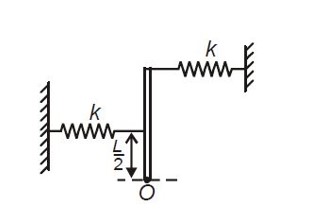
The given arrangement is in vertical plane and initially the springs are in natural length. The uniform rod is hinged at end O, about which it can freely rotate. The angular frequency of small oscillations of the rod is n/8 √(k/m). Find n. (Given: m = mass of rod, L = length of rod and k = mg/L)

Given mg = kL
∴ Iα = (kLθ.L + k (L/2)²θ - mg (L/2)θ)
(mL²/3)α = kL² (3/4)θ (restoring torque)
α = (9k/4m)θ
∴ ω = (3/2)√ (k/m)

For an SHM oscillator, the amplitude is 5 cm and its time period is 4 seconds. The minimum time taken by the particle to pass between points which are at distances 4 cm and 3 cm from the centre of oscillation on the same side of it will be

y = A sin (2πt/T)
t? - t? = (T/2π) [sin? ¹ (x? /A) - sin? ¹ (x? /A)]

Taking an Exam? Selecting a College?

Get authentic answers from experts, students and alumni that you won't find anywhere else.

On Shiksha, get access to

66K

Colleges

|

1.2K

Exams

|

6.9L

Reviews

|

1.8M

Answers

Learn more about...

Physics Oscillations 2025

Physics Oscillations 2025

View Exam Details

Most viewed information

Share Your College Life Experience

Didn't find the answer you were looking for?

Search from Shiksha's 1 lakh+ Topics

or

Ask Current Students, Alumni & our Experts

Quick Actions

Community GuidelinesUser Points System

QuestionsDiscussionsTags

Have a question related to your career & education?

or

See what others like you are asking & answering