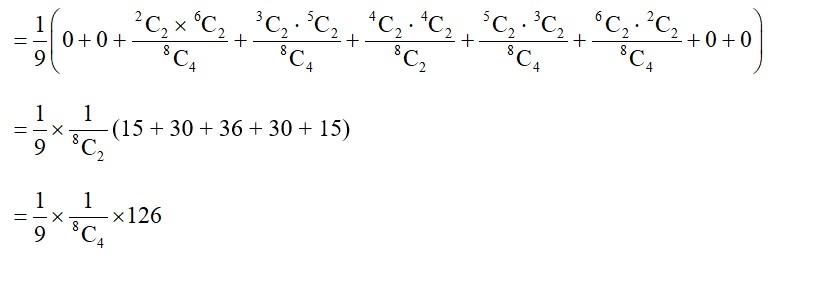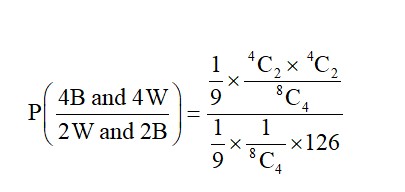Let B_i (i = 1, 2, 3) be three independent events in a sample space. The probability that only B₁ occurs is a, only B₂ occurs is b and B₃ occurs is  Let p be the probability that none of the events B₁ occurs and these 4 probabilities satisfy the equations (a - 2b) = ab and (b - 3 p =  (All the probabilities are assumed to lie in the integral (0, 1)). The  is equal to_________.

P (2 obtained on even numbered toss) = k (let)

P (2) = $\frac{1}{6}$  

P (  $\overline{2}$ )= $\frac{5}{6}$  

$k=\frac{5}{6}\times \frac{1}{6}+{\left(\frac{5}{6}\right)}^3\times \frac{1}{6}+{\left(\frac{5}{6}\right)}^5\times \frac{1}{6}+...$

$=\frac{\frac{5}{6}\times \frac{1}{6}}{1-{\left(\frac{5}{6}\right)}^2}$

$=\frac{5}{11}$

If x = 0, y = 6, 7, 8, 9, 10

If x = 1, y = 7, 8, 9, 10

If x = 2, y = 8, 9, 10

If x = 3, y = 9, 10

If x = 4, y = 10

If x = 5, y = no possible value

Total possible ways = (5 + 4 + 3 + 2 + 1) * 2

= 30

Required probability  $=\frac{30}{11*11}=\frac{30}{121}$

P (2W and 2B) = P (2B, 6W) × P (2W and 2B)

+ P (3B, 5W) × P (2W and 2B)

+ P (4B, 4W) × P (2W and 2B)

+ P (5B, 3W) × P (2W and 2B)

+ P (6B, 2W) × P (2W and 2B)

(15 + 30 + 36 + 30 + 15)

$=\frac{36}{126}$

$=\frac{18}{63}$

$=\frac{6}{21}$

$=\frac{2}{7}$

Let probability of tail is   $\frac{1}{3}$

⇒ Probability of getting head = $\frac{2}{3}$  

∴ Probability of getting 2 heads and 1 tail

$=\left(\frac{2}{3}\times \frac{2}{3}\times \frac{1}{3}\right)\times 3$

$=\frac{4}{27}\times 3$

$=\frac{4}{9}$                  

                  &nb

ax² + bx + c = 0

D = b² – 4ac

D = 0

b² – 4ac = 0

b² = 4ac

(i) AC = 1, b = 2 (1, 2, 1) is one way

(ii) AC = 4, b = 4

$\begin{array}{l}a=4c=1\\ a=2c=2\\ a=1c=4\end{array}\}3ways$

(iii) AC = 9, b = 6, a = 3, c = 3 is one way

1 + 3 + 1 = 5 way

Required probability = $\frac{5}{216}$