Let the tangent drawn to the parabola y² = 24x at the point (a, b) is perpendicular to the line 2x + 2y = 5. Then the normal to the hyperbola $\frac{x^2}{{\alpha }^2}-\frac{y^2}{{\beta }^2}=1$  at the point (a + 4, b + 4) does NOT pass through the point:

$?$ ae = 2b

$\frac{4b^2}{a^2}=e^2$  

Or 4 (1 – e²) = e²

4 = 5e² -> $e=\frac{2}{\sqrt[]{5}}$

If two circles intersect at two distinct points

->|r₁ – r₂| < C₁C₂ < r₁ + r₂

| r – 2| <  $\sqrt[]{9+16}$ < r + 2

|r – 2| < 5                     and r + 2 > 5

–5 < r – 2 < 5                    r > 3                      … (2)

–3 < r < 7                                                        … (1)

From (1) and (2)

3 < r < 7

x² – y² cosec²q = 5 $\frac{x^2}{1}-\frac{y^2}{si{n}^2\theta }=5$                        

x² cosec²q + y² = 5  $\frac{x^2}{si{n}^2\theta }+\frac{y^2}{1}=5$        

$e_H=\sqrt[]{7}{e}_e$                  

and $e_H=\sqrt[]{1+\frac{si{n}^2\theta }{1}}$ &n

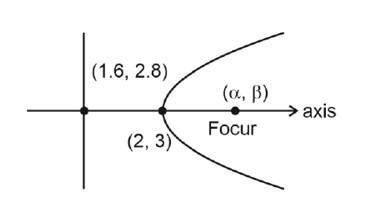
Slope of axis = $\frac{1}{2}$

$y-3=\frac{1}{2}\left(x-2\right)$              

⇒ 2y – 6 = x – 2

⇒ 2y – x – 4 = 0

2x + y – 6 = 0

4x + 2y – 12 = 0

            α + 1.6 = 4 ⇒ α = 2.4

            β + 2.8 = 6 ⇒

K $=\frac{4\sqrt[]{3}}{\sqrt[]{3}x+y}$ $\frac{\text{exception 25:}}{\text{exception 25:}}$

K = $\frac{\sqrt[]{3}x-y}{4\sqrt[]{3}}$ $\frac{\text{exception 25:}}{\text{exception 25:}}$

$\therefore \frac{4\sqrt[]{3}}{\sqrt[]{3}x+y}=\frac{\sqrt[]{3}x-y}{4\sqrt[]{3}}$

$\frac{x^2}{16}-\frac{y^2}{48}=1$

48 = 16 (e2 – 1)

$e=\sqrt[]{4}=2$