1.13 Explain how much portion of an atom located at (i) corner and (ii) body centre of a cubic unit cell is part of its neighbouring unit cell.
1.13 Explain how much portion of an atom located at (i) corner and (ii) body centre of a cubic unit cell is part of its neighbouring unit cell.
-
1 Answer
-
1.13 (i) An atom located at the corner of a cubic unit cell is shared by eight adjacent unit cells. Therefore, 1/8th portion of the atom is shared by one unit cell.
(ii) An atom located at the body centre of a cubic unit cell is not shared by its neighbouring unit cell. Therefore, the atom belongs only to the unit cell in which it is present i.e., its contribution to the unit cell is 1
Similar Questions for you
ΔG° = –RT * 2.303 log K
–nFE° = +RT * 2.303 log K
2 * 96500 * 0.295 = 8.314 * 298 * 2.303 log10 K
10 = log10 K = 1010
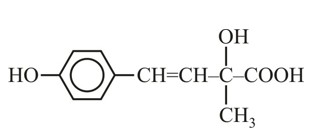
It has chiral centre and differently di substituted double bonded carbon atoms.
For FCC lattice
Packing efficiency = 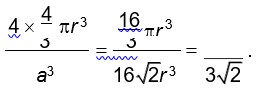
CsCl has BCC structure in which Cl– is present at corners of cube and Cs+ at body centre
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers