1.34 Calculate the efficiency of packing in case of a metal crystal for (i) Simple cubic (ii) Body-centred cubic (iii) Face-centred cubic (with the assumptions that atoms are touching each other).
1.34 Calculate the efficiency of packing in case of a metal crystal for (i) Simple cubic (ii) Body-centred cubic (iii) Face-centred cubic (with the assumptions that atoms are touching each other).
1.34 (i) The efficiency of packing in case of simple cubic unit cell is given below:
A simple cubic unit cell contains one atom per unit cell.
Also, a=2r, where a is the edge length and r is the radius of atom. Total volume of unit cell = a3
Packing efficiency = Volume of one sphere / Total volume of
Upvote 
Similar Questions for you
ΔG° = –RT * 2.303 log K
–nFE° = +RT * 2.303 log K
2 * 96500 * 0.295 = 8.314 * 298 * 2.303 log10 K
10 = log10 K = 1010
It has chiral centre and differently di substituted double bonded carbon atoms.
For FCC lattice
Packing efficiency =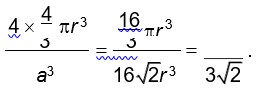 
CsCl has BCC structure in which Cl– is present at corners of cube and Cs+ at body centre
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else.
On Shiksha, get access to
Learn more about...
Chemistry Ncert Solutions Class 12th 2023
View Exam DetailsMost viewed information
SummaryDidn't find the answer you were looking for?
Search from Shiksha's 1 lakh+ Topics
Ask Current Students, Alumni & our Experts
Have a question related to your career & education?
See what others like you are asking & answering