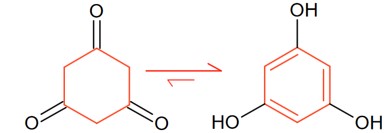
Which will have the highest enol content?
Which will have the highest enol content?
Aromaticity drives the highest enolic percentage of given structure:
Similar Questions for you
During removal of temporary hardness of water.
Due to common ion effect solubility of AgCl will decreases in KCl, AgCl and AgNO3 but in deionized water, no common ion effect will takes place so maximum solubility.
Remaining volume of solution = 400 ml
Mass of HNO3 = 25.2 – 11.5 = 13.7
Molarity = = 0.54 M = 54 × 10-2 M
Phenolphtalein is a pH dependant indicator. It is a weak acid which is colourless in acidic medium but gives pink colour in basic medium. The pink colour is due to its conjugate form. Phenolphthalein dissociates in basic medium. Therefore, assertion is true but reason is false.
At equilibrium rate of forward and backward reaction becomes equal.
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else.
On Shiksha, get access to
Learn more about...

Chemistry NCERT Exemplar Solutions Class 12th Chapter Six 2025
View Exam DetailsMost viewed information
SummaryDidn't find the answer you were looking for?
Search from Shiksha's 1 lakh+ Topics
Ask Current Students, Alumni & our Experts
Have a question related to your career & education?
See what others like you are asking & answering