Ask & Answer Question

Relations and Functions Ncert Solutions Maths class 12th Maths Class 12th Relations and Functions

10. Given an example of a relation. Which is

(i) Symmetric but neither reflexive nor transitive.

(ii) Transitive but neither reflexive nor symmetric.

(iii) Reflexive and symmetric but not transitive.

(iv) Reflexive and transitive but not symmetric.

(v) Symmetric and transitive but not reflexive.

19 Views | Posted 4 months ago

Asked by Shiksha User

1 Answer

Answered by

Vishal Baghel | Contributor-Level 10

4 months ago

Let A= ${a, b, c}$

(i) R= ${(a, b), (b, a)}$ is a relation in set A

So, $(a, b) \in R$ and $(b, a) \in R \to$ Symmetric

$(a, a) \notin R \to$ not reflexive

$(a, b) \in R, (b, a) \in R$ but $(a, a) \notin R$ $\to$ not transitive

(ii) R= ${(a, b), (b, c), (a, c)}$ is a relation in set A

So, $(a, a) \notin R \to$ not reflexive

$(a, b) \in R$ but $(b, a) \notin R \to$ not symmetric

$(a, b) \in R & (b, c) \in R$ and also $(a, c) \in R \to$ transitive

(iii) R= ${(a, a), (b, b), (c, c), (a, b), (b, a), (a, c), (c, a)}$

So, $(a, a), (b, b), (c, c) \in R \to$ Reflexive

$(a, b) \in R \to (b, a) \in R \to$ Symmetric

$(a, c) \in R \to (c, a) \in R$

$(b, a) \in R$ and $(a, c) \in R$

But $(b, c) \notin R \to$ not transitive

(iv) R= ${(a, a), (b, b), (c, c), (a, b), (b, c), (a, c)}$ is s relation in set A

So, $(a, a), (b, b), (c, c) \in R \to$ reflexive

$(a, b) & (b, c) \in R$ so, $(a, c) \in R \to$ transitive

$(a, b) \in R$ but $(b, a) \notin R \to$ not symmetric

(v) R= ${(a, a), (a, b), (b, a)}$

So, $(b, b) \notin R \to$ not reflexive

$(a, b) \in R$ and $(b, a) \in R \to$ symmetric

And $(a, b) \in R & (b, a) \in R$

and also $(a, a) \in R \to$ transitive

0 Upvotes 0 Downvotes

Similar Questions for you

Let S = {1, 2, 3 ,....,20}

R₁ = {(a, b) : a divide b}

R₂ = {(a, b) : a is integral multiple of b} a, b Î s

n(R₁ – R₂) = ?

alok kumar singh

R₁ = { (1, 1) (1, 2), (1, 3)., (1, 20), (2, 2), (2, 4). (2, 20), (3, 3), (3, 6), . (3, 18),
(4, 4), (4, 8), . (4, 20), (5, 5), (5, 10), (5, 15), (5, 20), (6, 6), (6, 12), (6, 18), (7. 7),
(7, 14), (8, 8), (8, 16), (9, 9), (9, 18), (10, 10), (10, 20), (11, 11), (12, 12), . (20, 20)}

n (R₁) = 66

R₂ = {a is integral multiple of b}

So n (R₁ – R₂) = 66 – 20 = 46

as R₁ Ç R₂ = { (a, a) : a Î s} = { (1, 1), (2, 2), ., (20, 20)}

$f (x) = {\begin{matrix} e^{- x}, & x < 0 \\ l n x, & x > 0 \end{matrix}$

$g (x) = {\begin{matrix} e^{x}, & x < 0 \\ x, & x > 0 \end{matrix}$

The gof : A->R is

alok kumar singh

$g o f (x) = {\begin{matrix} f (x), & f (x) < 0 \\ f (x), & f (x) > 0 \end{matrix}$

$= {\begin{array}{l} e^{l n x} = x & (0, 1) & e^{- x} \\ (- \infty, 0) & l n x & (1, \infty) \end{array}$

If A = {1, 2, 3, … 100}, R = {(x, y) | 2x = 3y, x, y ∈ A} is symmetric relation on A and the number of elements in R is n, the smallest integer value of n is

alok kumar singh

$?$ R is symmetric relation

⇒ (y, x) ∈ R V (x, y) ∈ R

(x, y) ∈ R ⇒ 2x = 3y and (y, x) ∈ R ⇒ 3x = 2y

Which holds only for (0, 0)

Which does not belongs to R.

∴ Value of n = 0

Let : f(0, R)->∞ be increasing function such that $\underset{x \to \infty}{l i m} \frac{f (7 x)}{f (x)} = 1$ then $\underset{x \to \infty}{l i m} (\frac{f (5 x)}{f (x)} - 1)$ is equal to

alok kumar singh

f is increasing function

x < 5x < 7x

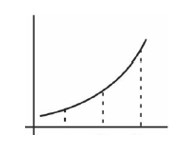
f (x) < f (5x) < f (7x)

$\frac{f (x)}{f (x)} < \frac{f (5 x)}{f (x)} < \frac{f (7 x)}{f (x)}$

$\underset{x \to \infty}{l i m} \frac{f (x)}{f (x)} < \underset{x \to \infty}{l i m} \frac{f (5 x)}{f (x)} < \underset{x \to \infty}{l i m} \frac{f (7 x)}{f (x)}$

-> $1 < \underset{x \to \infty}{l i m} \frac{f (5 x)}{f (x)} < 1$ $\underset{x \to \infty}{l i m} \frac{f (5 x)}{f (x)} = 1$

$\underset{x \to \infty}{l i m} (\frac{f (5 x)}{f (x)} - 1) = 0$

Let A = ${1, 2, 3, . . . . ., 10} a n d f : A \to A$ be defined as

$f (k) = {\begin{matrix} k + 1 & i f k i s o d d \\ k & i f k i s e v e n \end{matrix}$

Then the number of possible functions g : A ® A such that gof = f is:

alok kumar singh

Given f (k) = ${\begin{cases} k + 1, k i s o d d \\ k, k i s e v e n \end{cases}$

$? g : A \to A$ such that g (f (x) = f (x)

Case I : If x is even then g (x) = x . (i)

Case II : If x is odd then g (x + 1) = x + 1 . (ii)

From (i) & (ii), g (x) = x, when x is even

So total no. of functions = 10⁵ × 1 = 10⁵

Get authentic answers from experts, students and alumni that you won't find anywhere else

On Shiksha, get access to

65k Colleges
1.2k Exams
687k Reviews
1800k Answers

Community GuidelinesUser Points System

QuestionsDiscussionsTags

1 Answer

Similar Questions for you

Learn more about...

Most viewed information

Most viewed information

Share Your College Life Experience

Didn't find the answer you were looking for?

Need guidance on career and education? Ask our experts

Your Question

10. Given an example of a relation. Which is (i) Symmetric but neither reflexive nor transitive. (ii) Transitive but neither reflexive nor symmetric. (iii) Reflexive and symmetric but not transitive. (iv) Reflexive and transitive but not symmetric. (v) Symmetric and transitive but not reflexive.

1 Answer

Similar Questions for you

Learn more about...

Most viewed information

Most viewed information

Share Your College Life Experience

Didn't find the answer you were looking for?

Need guidance on career and education? Ask our experts

Your Question