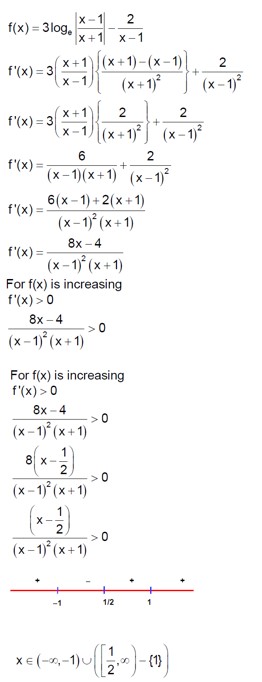113. Examine if Rolle’s Theorem is applicable to any of the following functions. Can you say something about the converse of Rolle’s Theorem from these examples?
for
for
for
113. Examine if Rolle’s Theorem is applicable to any of the following functions. Can you say something about the converse of Rolle’s Theorem from these examples?
for
for
for
-
1 Answer
-
113. Solution:
By Rolle’s Theorem, for a function if
f is continuous on
f is differentiable on
f(a)= f(b)
then, there exists some such that
therefore, Rolle’s Theorem is not applicable to those functions that do not satisfy any of the three conditions of the hypothesis.
for
It is evident that the given function f(x) is not continuous at every integral point.
In particular, f(x) is not continuous at x=5 and x=9
f(x) is not continuous in
Also,
The differentiability of f in is checked as follows.
Let n be an integer such that .
The left hand lim
...more
Similar Questions for you
f (x) is an even function
So, f (x) has at least four roots in (-2, 2)
So, g (x) has at least two roots in (-2, 2)
now number of roots of f (x)
It is same as number of roots of will have atleast 4 roots in (-2, 2)
Let
So, f(x) = x
Now,
f(x) = αx – b
option (D) satisfies
f (x) = f (6 – x) Þ f' (x) = -f' (6 – x) …. (1)
put x = 0, 2, 5
f' (0) = f' (6) = f' (2) = f' (4) = f' (5) = f' (1) = 0
and from equation (1) we get f' (3) = -f' (3)
So f' (x) = 0 has minimum 7 roots in
h (x) = f' (x) . f' (x)
h' (x) = (f' (x)2 + f' (x) f' (x)
h (x) = 0 has 13 roots in x
h' (x) = 0 has 12 roots in x
1 + x? - x? = a? (1+x)? + a? (1+x) + a? (1+x)² . + a? (1+x)?
Differentiate
4x³ - 5x? = a? + 2a? (1+x) + 3a? (1+x)².
12x² - 20x³ = 2a? + 6a? (1+x).
Put x = -1
12 + 20 = 2a? ⇒ a? = 16
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers