12. Show that the relation R defined in the set A of all triangles as R = {(T1, T2): T1 is similar to T2}, is equivalence relation. Consider three right angle triangles T1 with sides 3, 4, 5, T2 with sides 5, 12, 13 and T3 with sides 6, 8, 10. Which triangles among T1, T2 and T3 are related?

The given relation to set A of all triangles is defined asR= {(T1,T2):T1 is similar to T2}For T1∈A ,T1 is always similar to T1So, (T1,T1)∈R . Hence R is reflexive.For T1,T2∈A and (T1,T2)∈R we haveT1∼T2(similar)T2∼T1 i.e., (T2,T1)∈Rso, R is symmetric.for, T1,T2,T3∈A and (T1,T2)∈R and (T2,T3)∈RT1∼T2 and T2∼T3i.e., T1∼T3 →(T1,T3)∈Rso, R is transitive∴ R is an equivalence relation.Given, sides of T1 are 3,4,5Sides of T2 are 5,12,13Sides of T3 are 6,8,10As 35≠412≠513 we conclude that T1 is not similar to T2As 56≠128≠1310 we conclude that T2 is not similar to T3But as 36=48=510=12 we conclude that T1∼T3Hence, T1 is related to T3

Ask & Answer Question

Relations and Functions Ncert Solutions Maths class 12th Maths Class 12th Relations and Functions

12. Show that the relation R defined in the set A of all triangles as R = {(T₁, T₂): T₁ is similar to T₂}, is equivalence relation. Consider three right angle triangles T₁ with sides 3, 4, 5, T₂ with sides 5, 12, 13 and T₃ with sides 6, 8, 10. Which triangles among T₁, T₂ and T₃ are related?

13 Views | Posted 4 months ago

Asked by Shiksha User

1 Answer

Answered by

Vishal Baghel | Contributor-Level 10

4 months ago

The given relation to set A of all triangles is defined as

R= ${(T_{1}, T_{2}) : T_{1}$ is similar to $T_{2}}$

For $T_{1} \in A$ ,

$T_{1}$ is always similar to $T_{1}$

So, $(T_{1}, T_{1}) \in R$ . Hence R is reflexive.

For $T_{1,} T_{2} \in A$ and $(T_{1}, T_{2}) \in R$ we have

$T_{1} \sim T_{2} (s i m i l a r)$

$T_{2} \sim T_{1}$ i.e., $(T_{2}, T_{1}) \in R$

so, R is symmetric.

for, $T_{1}, T_{2}, T_{3} \in A$ and $(T_{1}, T_{2}) \in R$ and $(T_{2}, T_{3}) \in R$

$T_{1} \sim T_{2}$ and $T_{2} \sim T_{3}$

i.e., $T_{1} \sim T_{3}$ $\to (T_{1}, T_{3}) \in R$

so, R is transitive

$∴$ R is an equivalence relation.

Given, sides of $T_{1}$ are 3,4,5

Sides of $T_{2}$ are 5,12,13

Sides of $T_{3}$ are 6,8,10

As $\frac{3}{5} \neq \frac{4}{12} \neq \frac{5}{13}$ we conclude that $T_{1}$ is not similar to $T_{2}$

As $\frac{5}{6} \neq \frac{12}{8} \neq \frac{13}{10}$ we conclude that $T_{2}$ is not similar to $T_{3}$

But as $\frac{3}{6} = \frac{4}{8} = \frac{5}{10} = \frac{1}{2}$ we conclude that

...more

The given relation to set A of all triangles is defined as

R= ${(T_{1}, T_{2}) : T_{1}$ is similar to $T_{2}}$

For $T_{1} \in A$ ,

$T_{1}$ is always similar to $T_{1}$

So, $(T_{1}, T_{1}) \in R$ . Hence R is reflexive.

For $T_{1,} T_{2} \in A$ and $(T_{1}, T_{2}) \in R$ we have

$T_{1} \sim T_{2} (s i m i l a r)$

$T_{2} \sim T_{1}$ i.e., $(T_{2}, T_{1}) \in R$

so, R is symmetric.

for, $T_{1}, T_{2}, T_{3} \in A$ and $(T_{1}, T_{2}) \in R$ and $(T_{2}, T_{3}) \in R$

$T_{1} \sim T_{2}$ and $T_{2} \sim T_{3}$

i.e., $T_{1} \sim T_{3}$ $\to (T_{1}, T_{3}) \in R$

so, R is transitive

$∴$ R is an equivalence relation.

Given, sides of $T_{1}$ are 3,4,5

Sides of $T_{2}$ are 5,12,13

Sides of $T_{3}$ are 6,8,10

As $\frac{3}{5} \neq \frac{4}{12} \neq \frac{5}{13}$ we conclude that $T_{1}$ is not similar to $T_{2}$

As $\frac{5}{6} \neq \frac{12}{8} \neq \frac{13}{10}$ we conclude that $T_{2}$ is not similar to $T_{3}$

But as $\frac{3}{6} = \frac{4}{8} = \frac{5}{10} = \frac{1}{2}$ we conclude that $T_{1} \sim T_{3}$

Hence, $T_{1}$ is related to $T_{3}$

less

0 Upvotes 0 Downvotes

Similar Questions for you

Let S = {1, 2, 3 ,....,20}

R₁ = {(a, b) : a divide b}

R₂ = {(a, b) : a is integral multiple of b} a, b Î s

n(R₁ – R₂) = ?

alok kumar singh

R₁ = { (1, 1) (1, 2), (1, 3)., (1, 20), (2, 2), (2, 4). (2, 20), (3, 3), (3, 6), . (3, 18),
(4, 4), (4, 8), . (4, 20), (5, 5), (5, 10), (5, 15), (5, 20), (6, 6), (6, 12), (6, 18), (7. 7),
(7, 14), (8, 8), (8, 16), (9, 9), (9, 18), (10, 10), (10, 20), (11, 11), (12, 12), . (20, 20)}

n (R₁) = 66

R₂ = {a is integral multiple of b}

So n (R₁ – R₂) = 66 – 20 = 46

as R₁ Ç R₂ = { (a, a) : a Î s} = { (1, 1), (2, 2), ., (20, 20)}

$f (x) = {\begin{matrix} e^{- x}, & x < 0 \\ l n x, & x > 0 \end{matrix}$

$g (x) = {\begin{matrix} e^{x}, & x < 0 \\ x, & x > 0 \end{matrix}$

The gof : A->R is

alok kumar singh

$g o f (x) = {\begin{matrix} f (x), & f (x) < 0 \\ f (x), & f (x) > 0 \end{matrix}$

$= {\begin{array}{l} e^{l n x} = x & (0, 1) & e^{- x} \\ (- \infty, 0) & l n x & (1, \infty) \end{array}$

If A = {1, 2, 3, … 100}, R = {(x, y) | 2x = 3y, x, y ∈ A} is symmetric relation on A and the number of elements in R is n, the smallest integer value of n is

alok kumar singh

$?$ R is symmetric relation

⇒ (y, x) ∈ R V (x, y) ∈ R

(x, y) ∈ R ⇒ 2x = 3y and (y, x) ∈ R ⇒ 3x = 2y

Which holds only for (0, 0)

Which does not belongs to R.

∴ Value of n = 0

Let : f(0, R)->∞ be increasing function such that $\underset{x \to \infty}{l i m} \frac{f (7 x)}{f (x)} = 1$ then $\underset{x \to \infty}{l i m} (\frac{f (5 x)}{f (x)} - 1)$ is equal to

alok kumar singh

f is increasing function

x < 5x < 7x

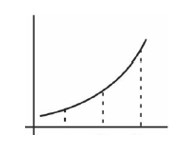
f (x) < f (5x) < f (7x)

$\frac{f (x)}{f (x)} < \frac{f (5 x)}{f (x)} < \frac{f (7 x)}{f (x)}$

$\underset{x \to \infty}{l i m} \frac{f (x)}{f (x)} < \underset{x \to \infty}{l i m} \frac{f (5 x)}{f (x)} < \underset{x \to \infty}{l i m} \frac{f (7 x)}{f (x)}$

-> $1 < \underset{x \to \infty}{l i m} \frac{f (5 x)}{f (x)} < 1$ $\underset{x \to \infty}{l i m} \frac{f (5 x)}{f (x)} = 1$

$\underset{x \to \infty}{l i m} (\frac{f (5 x)}{f (x)} - 1) = 0$

Let A = ${1, 2, 3, . . . . ., 10} a n d f : A \to A$ be defined as

$f (k) = {\begin{matrix} k + 1 & i f k i s o d d \\ k & i f k i s e v e n \end{matrix}$

Then the number of possible functions g : A ® A such that gof = f is:

alok kumar singh

Given f (k) = ${\begin{cases} k + 1, k i s o d d \\ k, k i s e v e n \end{cases}$

$? g : A \to A$ such that g (f (x) = f (x)

Case I : If x is even then g (x) = x . (i)

Case II : If x is odd then g (x + 1) = x + 1 . (ii)

From (i) & (ii), g (x) = x, when x is even

So total no. of functions = 10⁵ × 1 = 10⁵

Get authentic answers from experts, students and alumni that you won't find anywhere else

On Shiksha, get access to

65k Colleges
1.2k Exams
687k Reviews
1800k Answers

Community GuidelinesUser Points System

QuestionsDiscussionsTags

1 Answer

Similar Questions for you

Learn more about...

Most viewed information

Most viewed information

Share Your College Life Experience

Didn't find the answer you were looking for?

Need guidance on career and education? Ask our experts

Your Question