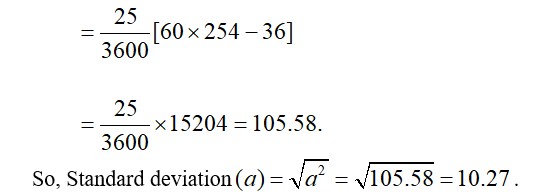21. Find the mean, variance and standard deviation using short-cut method
Height in cms
70-75
75-80
80-85
85-90
90-95
95-100
100-125
105-110
110-115
Frequencies
3
4
7
7
15
9
6
6
3
21. Find the mean, variance and standard deviation using short-cut method
|
Height in cms |
70-75 |
75-80 |
80-85 |
85-90 |
90-95 |
95-100 |
100-125 |
105-110 |
110-115 |
|
Frequencies |
3 |
4 |
7 |
7 |
15 |
9 |
6 |
6 |
3 |
-
1 Answer
-
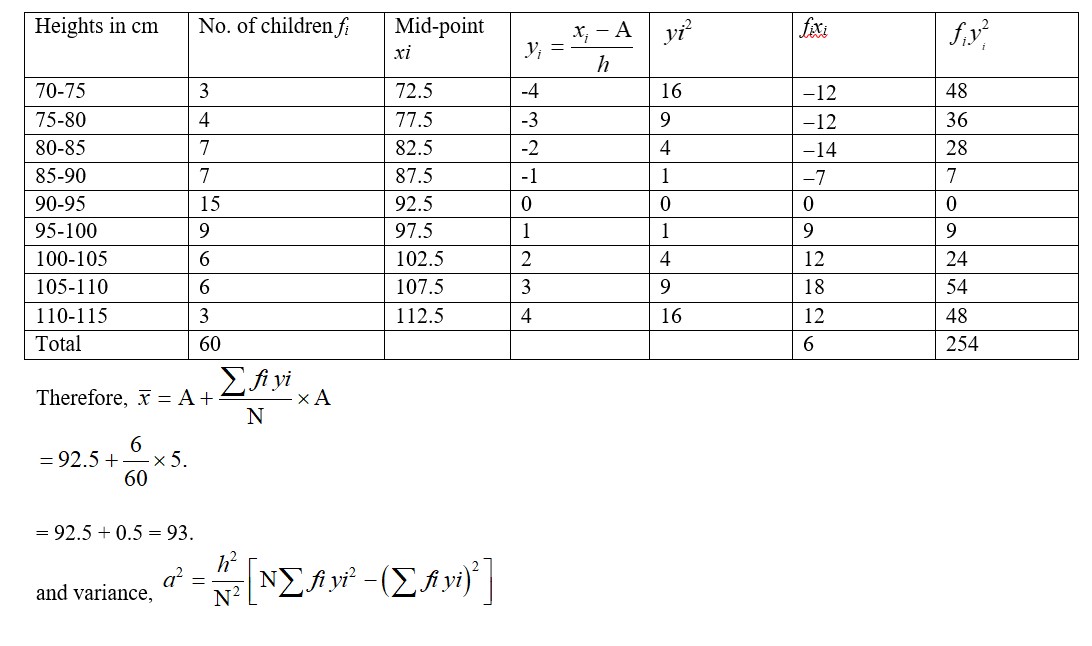
21. Let the assumed mean be A=92.5 and h=5
Similar Questions for you
Variance =
α2 + β2 = 897.7 * 8
= 7181.6
xi | fi | c.f. |
0 – 4 4 – 8 8 – 12 12 – 16 16 – 20 | 2 4 7 8 6 | 2 6 13 21 27 |
So, we have median lies in the class 12 – 16
I1 = 12, f = 8, h = 4, c.f. = 13
So, here we apply formula
20 M = 20 * 12.25
= 245
212 + a + b = 330
⇒ a + b = 118
= 3219
11760 + a2 + b2 = 19314
⇒ a2 + b2 = 19314 – 11760
= 7554
(a + b)2 –2ab = 7554
From here b = 41.795
a + b = 118
⇒ a + b + 2b = 118 + 83.59
= 201.59
Kindly go throuigh the solution
Given
&
(i) & (ii)
Now variance = 1 given
->(a - b) (a - b + 4) = 0
Since
Variance =
Let 2a2 – a + 1 = 5x
D = 1 – 4 (2) (1 – 5n)
= 40n – 7, which is not
As each square form is
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers