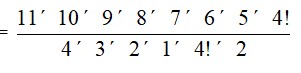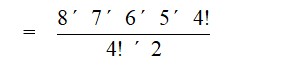21. In how many of the distinct permutations of the letters in MISSISSIPPI do the four I’s not come together?
21. In how many of the distinct permutations of the letters in MISSISSIPPI do the four I’s not come together?
-
1 Answer
-
21. There are 11 letters of which M appears 1 time, I appears 4 times, S appears 4 times and P appears 2 times.
The required number of arrangements =
= 11 * 10 * 9 * 5
= 34650
When the four I occurs together we treat them as single object IIII. This single object together with 7 remaining object will account for 8 object which have 1-M. 2-P and 4-S.
So, required number of permutation =
= 840
Therefore, total no. of permutation in which 4-I's do not come together
= 34650 – 840
= 33810
Similar Questions for you
Start with
(1)
(2)
(3) GTE : 4!, GTN: 4!, GTT : 4!
(4) GTWENTY = 1
⇒ 360 + 60 + 60 + 24 + 24 + 24 + 1 = 553
x + 2y + 3z = 42
0 x + 2y = 42 ->22 cases
1 x + 2y = 39 ->19 cases
2 x + 2y = 36 ->19 cases
3 x + 2y = 33 ->17 cases
4 x + 2y = 30 ->16 cases
5 x + 2y = 27 ->14 cases
6 x + 2y = 24 ->13 cases
7 x + 2y = 21 ->11 cases
8 x + 2y = 18 ->10 cases
9 x + 2y = 15 ->8 cases
10 x + 2y =12 -> 7 cases
11 x + 2y = 9 -> 5 cases
12 x + 2y = 6 -> 4 cases
13 x + 2y = 3 -> 2 cases
14 x + 2y = 0 -> 1 cases.
Total ways to partition 5 into 4 parts are:
5 0
4 1 0
3 2 0
3 1 0
2 1
51 Total way
After giving 2 apples to each child 15 apples left now 15 apples can be distributed in
15+3–1C2 = 17C2 ways
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers