23. Find the area of the region lying in the first quadrant and bounded by y = 4x2, x = 0, y = 1 and y = 4

Ask & Answer Question

Application of Integrals Ncert Solutions Maths class 12th Maths Class 12th Application of Integrals

23. Find the area of the region lying in the first quadrant and bounded by y = 4x², x = 0, y = 1 and y = 4

5 Views | Posted 5 months ago

Asked by Shiksha User

1 Answer

Answered by

Vishal Baghel | Contributor-Level 10

5 months ago

Given curve is $y = 4 x^{2} \Rightarrow x^{2} = \frac{1}{4} y$ - (1)

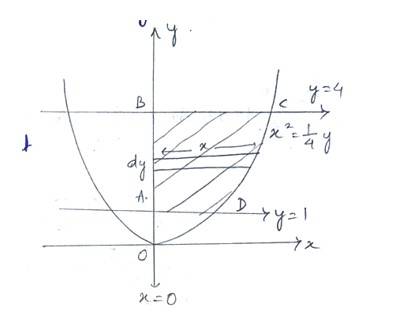
$x = 0$ i.e, y-axis and y=4 and y=1

Hence, the required area in Ist quadrant i.e, area ABCD = $\int_{y = 1}^{y = 4} x d y$

0 Upvotes 0 Downvotes

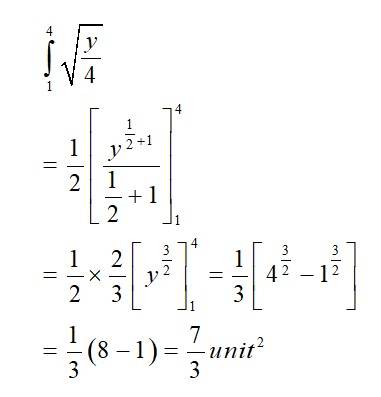
Similar Questions for you

Let a cure y = y(x) pass through the point (3, 3) and the area of the origin under this curve, above the x-axis and between the abscissae 3 and x (>3) be ${(\frac{y}{x})}^{3}$ . If the curve also passes through the point $(α, 6 \sqrt[]{10})$ in the first quadrant, then a is equal to………….

Raj Pandey

$\int_{3}^{x} f (x) d x = {(\frac{f (x)}{x})}^{3} \Rightarrow x^{3} \int_{3}^{x} f (x) d x = f^{3} (x),$ differentiating w.r.to x

$x^{3} f (x) + 3 x^{2} \frac{f^{3} (x)}{x^{3}} = 3 f^{2} (x) f' (x) \Rightarrow 3 y^{2} \frac{d y}{d x} = x^{3} y = \frac{3 y^{3}}{x} \Rightarrow 3 x y \frac{d y}{d x} = x^{4} + 3 y^{2}$

After solving we get $y^{2} = \frac{x^{4}}{3} + c x^{2}$ also curve passes through (3, 3) Þ c = -2

$∴ y^{2} = \frac{x^{4}}{3} - 2 x^{2}$ which passes through $(α, 6 \sqrt[]{10})$ $∴ \frac{α^{4} - 6 α^{2}}{3} = 360 \Rightarrow α = 6$

The odd natural number a, such that the area of the region bounded by y = 1, y = 3, x = 0, x = y^a is $\frac{364}{3},$ is equal to:

Raj Pandey

Since a is a odd natural number then $| \int_{1}^{3} y^{a} d y | = \frac{364}{3} \Rightarrow | {(\frac{y^{a + 1}}{a + 1})}_{1}^{3} | = \frac{364}{3} \Rightarrow \frac{3^{a + 1}}{a + 1} = \frac{364}{3}$