27. (i)
Find equation of line joining (1, 2) and (3, 6) using determinants.
(ii) Find equation of line joining (3, 1) and (9, 3) using determinants
27. (i) Find equation of line joining (1, 2) and (3, 6) using determinants.
(ii) Find equation of line joining (3, 1) and (9, 3) using determinants
-
1 Answer
-
(i) Let P (x, y) be any point on line joining A (1, 2) & B (3, 6)
Then, area of triangle (ABP) = 0 {the point are collinear
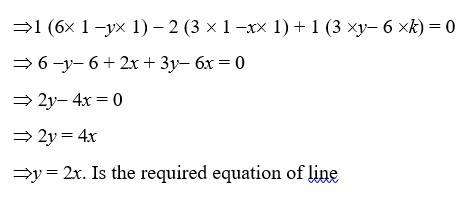
Similar Questions for you
|2A| = 27
8|A| = 27
Now |A| = α2–β2 = 24
α2 = 16 + β2
α2– β2 = 16
(α–β) (α+β) = 16
->α + β = 8 and
α – β = 2
->α = 5 and β = 3
|A| = 3
|B| = 1
->|C| = |ABAT| = |A|B|A7| = |A|2|B|
= 9
->|X| = |A|C|2|AT|
= 3 * 92 * 3 = 9 * 92 = 729
|A| = 2
->
->, m ¬ even
7
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers
