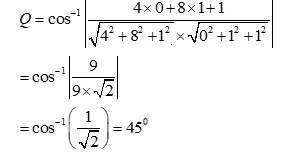Ncert Solutions Maths class 12th Maths Class 12th Three Dimensional Geometry

36. In the following cases, determine whether the given planes are parallel or perpendicular and in case they are neither, find the angle between them.

$\begin{array}{l} \end{array} (a) 7 x + 5 y + 6 z + 30 = 0 a n d 3 x - y - 10 z + 4 = 0$

$(b) 2 x + y + 3 z - 2 = 0 a n d x - 2 y + 5 = 0$

$(c) 2 x - 2 y + 4 z + 5 = 0 a n d 3 x - 3 y + 6 z - 1$

$(d) 2 x - y + 3 z - 1 = 0 a n d 2 x - y + 3 z + 3 = 0$

$(e) 4 x + 8 y + z - 8 = 0 a n d y + z - 4 = 0$

3 Views | Posted 4 months ago

1 Answer

Answered by

Vishal Baghel | Contributor-Level 10

4 months ago

The direction ratios of normal to the plane, $L_{1} : a_{1} x + b_{1} y + c_{1} z = 0 .$ , are $a_{1}, b_{1}, c_{1}$ and $L_{2} : a_{2} x + b_{2} y + c_{2} z = 0 .$

$L_{1}$
$\begin{array}{l} L_{2}, i f \frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} = \frac{c_{1}}{c_{2}} \\ L_{1} ⊥ L_{2}, i f a_{1} a_{2} + b_{1} b_{2} + c_{1} c_{2} = 0 \end{array}$

The angle between $L_{1} & L_{2}$ is given by,

(b) The equations of the planes are $2 x + y + 3 z - 2 = 0 a n d x - 2 y + 5 = 0$

$\begin{array}{l} a_{1} = 2, b_{1} = 1, c_{1} = 3 & a_{2} =, b_{2} = - 2, c_{2} = \\ a_{1} a_{2} + b_{1} b_{2} + c_{1} c_{2} = 2 \times 1 + 1 \times (- 2) + 3 \times 0 = 0 \end{array}$

Thus, the given planes are perpendicular to each other.

(c) The equations of the given planes are $2 x - 2 y + 4 z + 5 = 0 a n d 3 x - 3 y + 6 z - 1$

Here, $a_{1} = 2, b_{1} = - 2, c_{1} = 4 & a_{2} =, b_{2} = - 3, c_{2} = 6$

$a_{1} a_{2} + b_{1} b_{2} + c_{1} c_{2} = 2 \times 3 + 1 \times (- 2) (- 3) + 4 \times 6 = 6 + 6 + 24 = 36 \neq 0$

Thus, the given planes are not perpendicular to each other.

$\begin{array}{l} \frac{a_{1}}{a_{2}} = \frac{2}{3}, \frac{b_{1}}{b_{2}} = \frac{- 2}{- 3} = \frac{2}{3} & \frac{c_{1}}{c_{2}} = \frac{4}{6} = \frac{2}{3} \\ ∴ \frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} = \frac{c_{1}}{c_{2}} \end{array}$

Thus, the given planes are parallel to each other

(d) The equations of the planes are and $2 x - y + 3 z - 1 = 0 a n d 2 x - y + 3 z + 3 = 0$

$\begin{array}{l} a_{1} = 2, b_{1} = - 1, c_{1} = 3 & a_{2} =, b_{2} = - 1, c_{2} = 3 \\ \frac{a_{1}}{a_{2}} = \frac{2}{2} = 1, \frac{b_{1}}{b_{2}} = \frac{- 1}{- 1} = 1 & \frac{c_{1}}{c_{2}} = \frac{3}{3} = 1 \\ ∴ \frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} = \frac{c_{1}}{c_{2}} \end{array}$

Thus, the given lines are parallel to each other

(e) The equations of the given planes are $4 x + 8 y + z - 8 = 0 a n d y + z - 4 = 0$ $\begin{array}{l} a_{1} = 4, b_{1} = 8, c_{1} = 1 & a_{2} =, b_{2} = 1, c_{2} = 1 \\ a_{1} a_{2} + b_{1} b_{2} + c_{1} c_{2} = 4 \times 0 + 8 \times 1 + 1 = 9 \neq 0 \end{array}$

Therefore, the given lines are not perpendicular to each

...more

The direction ratios of normal to the plane, $L_{1} : a_{1} x + b_{1} y + c_{1} z = 0 .$ , are $a_{1}, b_{1}, c_{1}$ and $L_{2} : a_{2} x + b_{2} y + c_{2} z = 0 .$

$L_{1}$
$\begin{array}{l} L_{2}, i f \frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} = \frac{c_{1}}{c_{2}} \\ L_{1} ⊥ L_{2}, i f a_{1} a_{2} + b_{1} b_{2} + c_{1} c_{2} = 0 \end{array}$

The angle between $L_{1} & L_{2}$ is given by,

(b) The equations of the planes are $2 x + y + 3 z - 2 = 0 a n d x - 2 y + 5 = 0$

$\begin{array}{l} a_{1} = 2, b_{1} = 1, c_{1} = 3 & a_{2} =, b_{2} = - 2, c_{2} = \\ a_{1} a_{2} + b_{1} b_{2} + c_{1} c_{2} = 2 \times 1 + 1 \times (- 2) + 3 \times 0 = 0 \end{array}$

Thus, the given planes are perpendicular to each other.

(c) The equations of the given planes are $2 x - 2 y + 4 z + 5 = 0 a n d 3 x - 3 y + 6 z - 1$

Here, $a_{1} = 2, b_{1} = - 2, c_{1} = 4 & a_{2} =, b_{2} = - 3, c_{2} = 6$

$a_{1} a_{2} + b_{1} b_{2} + c_{1} c_{2} = 2 \times 3 + 1 \times (- 2) (- 3) + 4 \times 6 = 6 + 6 + 24 = 36 \neq 0$

Thus, the given planes are not perpendicular to each other.

Thus, the given planes are parallel to each other

(d) The equations of the planes are and $2 x - y + 3 z - 1 = 0 a n d 2 x - y + 3 z + 3 = 0$

Thus, the given lines are parallel to each other

Therefore, the given lines are not perpendicular to each other.

$\begin{array}{l} \frac{a_{1}}{a_{2}} = \frac{4}{0}, \frac{b_{1}}{b_{2}} = \frac{8}{1} = 8 & \frac{c_{1}}{c_{2}} = \frac{1}{1} = 1 \\ ∴ \frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}} \end{array}$

Therefore, the given lines are not parallel to each other.

The angle between the planes is given by,

less

0 Upvotes 0 Downvotes

Similar Questions for you

If $\int_{}^{} (\frac{x^{2} c o s x}{1 + π^{x}} + \frac{1 + s i n^{2} x}{1 + e^{{(s i n x)}^{2023}}}) d x = \frac{π}{4} (π + α) - 2$

Then the value of 'α' is equal to

alok kumar singh

$\int_{- \frac{π}{2}}^{\frac{π}{2}} (\frac{x^{2} c o s x}{1 + π^{2}} + \frac{1 + s i n^{2} x}{1 + e^{{(s i n x)}^{2023}}}) d x = \frac{π}{4} (π + α) - 2$

$\int_{0}^{\frac{π}{2}} {(\frac{x^{2} c o s x}{1 + π^{x}} + \frac{1 + s i n^{2} x}{1 + e^{{(s i n x)}^{2023}}}) + (\frac{x^{2} c o s x}{1 + π^{- x}} + \frac{1 + s i n^{2} x}{1 + e^{- {(s i n x)}^{2023}}})} d x$

$= \frac{π}{4} (π + α) - 2$

$\int_{0}^{\frac{π}{2}} (x^{2} c o s x + 1 + s i n^{2} x) d x = \frac{π}{4} (π + α) - 2$

$\int_{0}^{\frac{π}{2}} x^{2} c o s x d x + \int_{0}^{\frac{π}{2}} (1 + s i n^{2} x) d x = \frac{π}{4} (π + α) - 2$ ....(1)

Let $I_{1} = \int_{0}^{\frac{π}{2}} (1 + s i n^{2} x) d x$

$I_{1} = \int_{0}^{\frac{π}{2}} 1 \cdot d x + \int_{0}^{\frac{π}{2}} (\frac{1 - c o s 2 x}{2}) d x$

$I_{1} = \frac{π}{2} + \frac{1}{2} [\frac{π}{2} + 0]$

$I_{1} = \frac{3 π}{4}$

Let $I_{2} = \int_{0}^{\frac{π}{2}} x^{2} c o s x d x$

$I_{2} = {[x^{2} (s i n x) - \int 2 x \int c o s x d x]}_{0}^{\frac{π}{2}}$

$I_{2} = {[x^{2} (s i n x) - 2 \int x s i n x]}_{0}^{\frac{π}{2}}$

$I_{2} = {[x^{2} s i n x - 2 (x (- c o s x) + \int c o s x)]}_{0}^{\frac{π}{2}}$

$I_{2} = {[x^{2} s i n x - 2 (- x c o s x + s i n x)]}_{0}^{\frac{π}{2}}$

$I_{2} = (\frac{π^{2}}{4} - 2)$

Put l₁ and l₂ in (1)

$\frac{π^{2}}{4} - 2 + \frac{3 π}{4}$

$\frac{π^{2}}{4} + \frac{3 π}{4} - 2$

$\frac{π}{4} (π + 3) - 2$

α = 3

If $| \vec{a} | = 1$ , $| \vec{b} | = 4$ $\vec{a} \cdot \vec{b} = 2$ and $\vec{c} = 2 (\vec{a} \times \vec{b}) - 3 \vec{b}$ Then the angle between $\vec{b}$ and $\vec{c}$ is

alok kumar singh

Given $| \vec{a} | = 1$ , $| \vec{b} | = 4$ , $\vec{a} \cdot \vec{b} = 2$

$\vec{c} = 2 (\vec{a} \times \vec{b}) - 3 \vec{b}$

Dot product with $\vec{a}$ on both sides

$\vec{c} \cdot \vec{a} = - 6$ ... (1)

Dot product with $\vec{b}$ on both sides

$\vec{b} \cdot \vec{c} = - 48$ ... (2)

$\vec{c} \cdot \vec{c} = 4 {| \vec{a} \times \vec{b} |}^{2} + 9 {| \vec{b} |}^{2}$

${| \vec{c} |}^{2} = 4 [{| \vec{a} |}^{2} \cdot {| \vec{b} |}^{2} - {(\vec{a} \cdot \vec{b})}^{2}] + 9 {| \vec{b} |}^{2}$

${| \vec{c} |}^{2} = 4 [(1) {(4)}^{2} - (4)] + 9 (16)$

${| \vec{c} |}^{2} = 4 [12] + 144$

${| \vec{c} |}^{2} = 48 + 144$

${| \vec{c} |}^{2} = 192$

$c o s θ = \frac{\vec{b} \cdot \vec{c}}{| \vec{b} | | \vec{c} |}$

$c o s θ = \frac{- 48}{\sqrt[]{192} \cdot 4}$

$c o s θ = \frac{- 48}{8 \sqrt[]{3} \cdot 4}$

$c o s θ = \frac{- 3}{2 \sqrt[]{3}}$

$c o s θ = \frac{- \sqrt[]{3}}{2}$ $θ = c o s^{- 1} (\frac{- \sqrt[]{3}}{2})$

If the foot of perpendicular from (1, 2, 3) to the line $\frac{x + 1}{2} = \frac{y - 2}{5} = \frac{z - 4}{1}$ is (a, b, g) then find a + b + g

alok kumar singh

(a – 1) × 2 + (b – 2) × 5 + (g – 3) × 1 = 0

2a + 5b + g – 15 = 0

Also, P lie on line

a + 1 = 2λ

b – 2 = 5λ

g – 4 = λ

2 (2λ – 1) + 5 (5λ + 2) + λ + 4 – 15 = 0

4λ + 25λ + λ – 2 + 10 + 4 – 15 = 0

30λ – 3 = 0

$λ = \frac{1}{10}$

a + b + g = (2λ – 1) + (5λ + 2) + (λ + 4)

$= 8 λ + 5 = \frac{8}{10} + 5 = 5.8$

If (α, β, γ) is mirror image of the point (2, 3, 4) with respect to the line $\frac{x - 1}{2} = \frac{y - 2}{3} = \frac{z - 3}{4}$ Then 2α + 3β + 4γ is

alok kumar singh

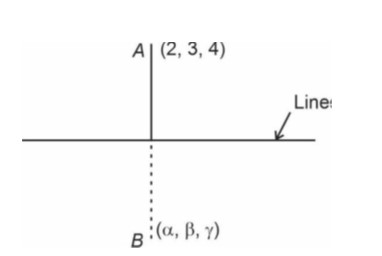
Take $\frac{x - 1}{2} = \frac{y - 2}{3} = \frac{z - 3}{4} = λ$

x = 2λ + 1, y = 3λ + 2, z = 4λ + 3

$\vec{A B}$ = (α − 2) $\hat{i}$ + (β − 3) $\hat{j}$ + (γ − 4) $\hat{k}$

Now,

(α − 2) ⋅ 2 + (β − 3) ⋅3 + (γ − 4) ⋅ 4 = 0

2α − 4 + 3β − 9 + 4γ −16 = 0

⇒ 2α + 3β + 4γ = 29

Let $λ$ be an integer. IF the shortest distance between the lines $x - λ = 2 y - 1 = - 2 z$ and $x = y + 2 λ = z - λ i s \frac{\sqrt[]{7}}{2 \sqrt[]{2}}$ , then the value of $| λ | i s . . . . . . . . . . . . . . . . . . .$

Vishal Baghel

$L_{1} = \frac{x - λ}{1} = \frac{y - \frac{1}{2}}{\frac{1}{2}} = \frac{z}{- \frac{1}{2}}$

$∴ S D = \frac{| - 2 λ + 3 (2 λ + \frac{1}{2}) + λ |}{\sqrt[]{14}} = \frac{| 5 λ + \frac{3}{2} |}{\sqrt[]{14}}$

$5 λ + \frac{3}{2} = - \frac{7}{2} \Rightarrow 5 λ = - 5 \Rightarrow λ = - 1$

$∴ | λ | = 1$

Get authentic answers from experts, students and alumni that you won't find anywhere else

On Shiksha, get access to

65k Colleges
1.2k Exams
688k Reviews
1800k Answers

Community GuidelinesUser Points System

QuestionsDiscussionsTags

1 Answer

Similar Questions for you

Learn more about...

Most viewed information

Share Your College Life Experience

Didn't find the answer you were looking for?

Need guidance on career and education? Ask our experts

Your Question