37. Choose the correct answer:
The area bounded by the curve y = x|x|, axis and the ordinates x = –1 and x = 1 is given by:
[Hint: y = x2 if x > 0 and y = –x2 if x < 0]
(A) 0
(B) 1/3
(C) 2/3
(D) 4/3
37. Choose the correct answer:
The area bounded by the curve y = x|x|, axis and the ordinates x = –1 and x = 1 is given by:
[Hint: y = x2 if x > 0 and y = –x2 if x < 0]
(A) 0
(B) 1/3
(C) 2/3
(D) 4/3
-
1 Answer
-
The given curve is
Which is in the form of a parabola nad the lines are
At
At
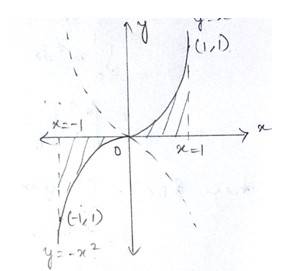
Shaded area of the Ist quadrant
Shaded area of the IInd quadrant
Total area of the enclosed region
Option (c) is correct.
Similar Questions for you
A = ∫? ² lnx dx = 2ln2 – 1
A' = 4 - 2 (2ln2 – 1) = 6 – 4ln2
y = |x − 1|, y = 3 – |x|
(A graph is shown with vertices A (1, 0), B (2, 1), C (0, 3), D (-1, 2). The lines are y = x - 1, y = 3 - x, y = 3 + x, and y = -x + 1)
AB = √2, BC = 2√2
⇒ Area = 4 sq. units
Required area (above x-axis)
A? = 2∫? (8/2 - x - √x)dx
= 2 [16 - 16/4 - 8/3*2] = 40/3
and A? = 4 (1/2 k²) = 2k²
∴ 27 * (40/3) = 5 * (2k²)
=> k = 6
for above x-axis.
We are given bounds for a function f (t) on two intervals and need to find the range of g (3) = ∫? ³ f (t) dt.
We split the integral: g (3) = ∫? ¹ f (t)dt + ∫? ³ f (t)dt.
For the first interval t ∈ [0, 1], we have 1/3 ≤ f (t) ≤ 1. Integrating from 0 to 1 gives:
∫? ¹ (1/3) dt ≤ ∫? ¹ f (t)dt ≤ ∫? ¹ 1 dt ⇒ 1/3 ≤ ∫? ¹ f (t)dt ≤ 1.
For the second interval t ∈ (1, 3], we have 0 ≤ f (t) ≤ 1/2. Integrating from 1 to 3 gives:
∫? ³ 0 dt ≤ ∫? ³ f (t)dt ≤ ∫? ³ (1/2) dt ⇒ 0 ≤ ∫? ³ f (t)dt ≤ (1/2) (3
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers
