38. If the vertices A, B, C of a triangle ABC are (1, 2, 3), (–1, 0, 0), (0, 1, 2), respectively, then find ∠ABC. [∠ABC is the angle between the vectors and ]
38. If the vertices A, B, C of a triangle ABC are (1, 2, 3), (–1, 0, 0), (0, 1, 2), respectively, then find ∠ABC. [∠ABC is the angle between the vectors and ]
Vertices of are given as
is the angle between the vectors and
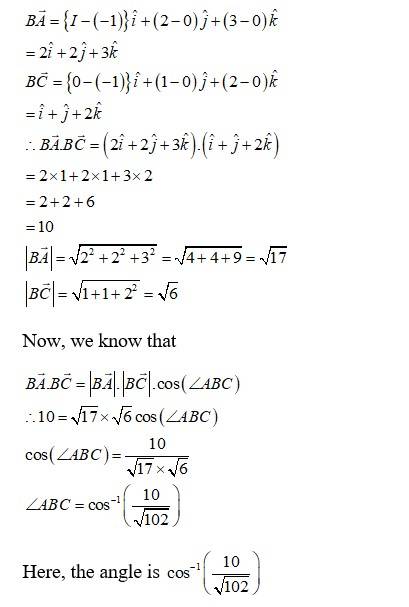
Similar Questions for you
6.00
b·a = c·a
|a+b-c|² = |a|²+|b|²+|c|²+2(a·b - b·c - a·c)
= 4+16+16+2(a·b - 0 - a·b) = 36
⇒ |a+b-c| = 6
(a+3b). (7a-5b) = 7|a|² - 5ab + 21ab - 15|b|² = 7|a|²+16ab-15|b|²=0.
(a-4b). (7a-2b) = 7|a|² - 2ab - 28ab + 8|b|² = 7|a|²-30ab+8|b|²=0.
Subtracting: 46ab - 23|b|² = 0 ⇒ 2ab = |b|².
Substituting: 7|a|² + 8|b|² - 15|b|² = 0 ⇒ 7|a|² = 7|b|² ⇒ |a|=|b|.
cosθ = ab/ (|a|b|) = ab/|b|² = (1/2)|b|²/|b|² = 1/2.
θ
a×b=c ⇒ a.c=0, b.c=0.
|c|² = |a|²|b|² - (a.b)² = (3)|b|² - 1. |c|=√2. So |b|²=1, |b|=1.
Projection of b on a×c.
a×c = a× (a×b) = (a.b)a - (a.a)b = a - 3b.
|a-3b|² = |a|²+9|b|²-6 (a.b) = 3+9-6 = 6.
l = |b. (a-3b)|/|a-3b| = | (a.b)-3|b|²|/√6 = |1
|a × b|² + |a . b|² = |a|²|b|²
8² + (a . b)² = 2² * 5²
64 + (a . b)² = 100
(a . b)² = 36
a . b = 6 (since angle seems acute from options, but could be -6).
a = i + j + 2k
b = -i + 2j + 3k
a + b = 3j + 5k
a . b = -1 + 2 + 6 = 7
a × b = |i, j, k; 1, 2; -1, 2, 3| = -i - 5j + 3k
(a - b) × b) = (a × b) - (b × b) =
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else.
On Shiksha, get access to
Learn more about...
Didn't find the answer you were looking for?
Search from Shiksha's 1 lakh+ Topics
Ask Current Students, Alumni & our Experts
Have a question related to your career & education?
See what others like you are asking & answering

