<p><strong>39. If <math><mrow><msub><mrow><mi>l</mi></mrow><mrow><mn>1</mn></mrow></msub><mo>,</mo><mo> </mo><msub><mrow><mi>m</mi></mrow><mrow><mn>1</mn></mrow></msub><mo>,</mo><mo> </mo><msub><mrow><mi>n</mi></mrow><mrow><mn>1</mn></mrow></msub><mo> </mo><mi>a</mi><mi>n</mi><mi>d</mi><mo> </mo><msub><mrow><mi>l</mi></mrow><mrow><mn>2</mn></mrow></msub><mo>,</mo><mo> </mo><msub><mrow><mi>m</mi></mrow><mrow><mn>2</mn></mrow></msub><mo>,</mo><mo> </mo><msub><mrow><mi>n</mi></mrow><mrow><mn>2</mn></mrow></msub><mo> </mo></mrow></math> are the direction cosines of two mutually perpendicular lines, show that the direction cosines of the line perpendicular to both of these are <math><mrow><msub><mrow><mi>m</mi></mrow><mrow><mn>1</mn></mrow></msub><msub><mrow><mi>n</mi></mrow><mrow><mn>2</mn></mrow></msub><mo> </mo><mo>−</mo><mo> </mo><msub><mrow><mi>m</mi></mrow><mrow><mn>2</mn></mrow></msub><msub><mrow><mi>n</mi></mrow><mrow><mn>1</mn></mrow></msub><mo>,</mo><mo> </mo><msub><mrow><mi>n</mi></mrow><mrow><mn>1</mn></mrow></msub><msub><mrow><mi>l</mi></mrow><mrow><mn>2</mn></mrow></msub><mo> </mo><mo>−</mo><mo> </mo><msub><mrow><mi>n</mi></mrow><mrow><mn>2</mn></mrow></msub><msub><mrow><mi>l</mi></mrow><mrow><mn>1</mn></mrow></msub><mo>,</mo><mo> </mo><msub><mrow><mi>l</mi></mrow><mrow><mn>1</mn></mrow></msub><msub><mrow><mi>m</mi></mrow><mrow><mn>2</mn></mrow></msub><mo> </mo><mo></mo><mo>−</mo><mo> </mo><msub><mrow><mi>l</mi></mrow><mrow><mn>2</mn></mrow></msub><msub><mrow><mi>m</mi></mrow><mrow><mn>1</mn></mrow></msub><mo>.</mo></mrow></math></strong></p>

It is given that l1, m1, n1 and l2, m2, n2 are the direction cosines of two mutually perpendicular lines. Therefore,l1l2+m1m2+n1 n2=0..........(1)l12+m12+n1 2=1..........(2)l22+m22+n2 2=1..........(3)Let l, m, n be the direction cosines of the line which is perpendicular to the line with direction cosines l1, m1, n1 and l2, m2, n2.∴ll1+ mm1+ nn1 =0l l2+m m2+n n2=0∴lm1n2−m2n1=mn1l2−n2l1=nl1m2−l2m1⇒l2(m1n2−m2n1)2=m2(n1l2−n2l1)2=n2(l1m2−l2m1)2⇒l2(m1n2−m2n1)2=m2(n1l2−n2l1)2=n2(l1m2−l2m2)2=l2+m2+n2(m1n2−m2n1)2+(n1l2−n2l1)2+(l1m2−l2m2)2..........(4)l, m, n are the direction cosines of the line.∴l2 + m2 + n2 =1…(5)It is known that,(l12+m12+n1 2)(l22+m22+n2 2)−(l1l2+m1m2+n1 n2)2=(m1n2−m2n1)2+(n1l2−n2l1)2+(l1m2−l2m1)2From,(1),(2)&(3),we.obtain⇒1.1−0=(m1n2−m2n1)2+(n1l2−n2l1)2+(l1m2−l2m1)2∴(m1n2−m2n1)2+(n1l2−n2l1)2+(l1m2−l2m1)2=1..........(6)Substituting the values from equations (5) and (6) in equation (4), we obtainl2(m1n2−m2n1)2=m2(n1l2−n2l1)2=n2(l1m2−l2m1)2=1Thus, the direction cosines of the required line are m1n2−m2n1,n1l2−n2l1,l1m2−l2m1

Ask & Answer Question

Ncert Solutions Maths class 12th Maths Class 12th Three Dimensional Geometry

39. If $l_{1}, m_{1}, n_{1} a n d l_{2}, m_{2}, n_{2}$ are the direction cosines of two mutually perpendicular lines, show that the direction cosines of the line perpendicular to both of these are $m_{1} n_{2} - m_{2} n_{1}, n_{1} l_{2} - n_{2} l_{1}, l_{1} m_{2} - l_{2} m_{1} .$

10 Views | Posted 4 months ago

Asked by Shiksha User

1 Answer

Answered by

Vishal Baghel | Contributor-Level 10

4 months ago

It is given that $l_{1}, m_{1}, n_{1} a n d l_{2}, m_{2}, n_{2}$ are the direction cosines of two mutually perpendicular lines. Therefore,

$\begin{array}{l} l_{1} l_{2} + m_{1} m_{2} + n_{1} n_{2} = 0 . . . . . . . . . . (1) \\ {l_{1}}^{2} + {m_{1}}^{2} + n_{1}^{2} = 1 . . . . . . . . . . (2) \\ {l_{2}}^{2} + {m_{2}}^{2} + n_{2}^{2} = 1 . . . . . . . . . . (3) \end{array}$

Let $l, m, n$ be the direction cosines of the line which is perpendicular to the line with direction cosines $l_{1}, m_{1}, n_{1} a n d l_{2}, m_{2}, n_{2} .$

$\begin{array}{l} ∴ l l_{1} + m m_{1} + n n_{1} = 0 \\ l l_{2} + m m_{2} + n n_{2} = 0 \\ ∴ \frac{l}{m_{1} n_{2} - m_{2} n_{1}} = \frac{m}{n_{1} l_{2} - n_{2} l_{1}} = \frac{n}{l_{1} m_{2} - l_{2} m_{1}} \\ \Rightarrow \frac{l^{2}}{{(m_{1} n_{2} - m_{2} n_{1})}^{2}} = \frac{m^{2}}{{(n_{1} l_{2} - n_{2} l_{1})}^{2}} = \frac{n^{2}}{{(l_{1} m_{2} - l_{2} m_{1})}^{2}} \\ \Rightarrow \frac{l^{2}}{{(m_{1} n_{2} - m_{2} n_{1})}^{2}} = \frac{m^{2}}{{(n_{1} l_{2} - n_{2} l_{1})}^{2}} = \frac{n^{2}}{{(l_{1} m_{2} - l_{2} m_{2})}^{2}} \\ = \frac{l^{2} + m^{2} + n^{2}}{{(m_{1} n_{2} - m_{2} n_{1})}^{2} + {(n_{1} l_{2} - n_{2} l_{1})}^{2} + {(l_{1} m_{2} - l_{2} m_{2})}^{2}} . . . . . . . . . . (4) \end{array}$

$l, m, n$ are the direction cosines of the line.

$∴ l^{2} + m^{2} + n^{2} = 1 \dots (5)$

It is known that,

$\begin{array}{l} ({l_{1}}^{2} + {m_{1}}^{2} + n_{1}^{2}) ({l_{2}}^{2} + {m_{2}}^{2} + n_{2}^{2}) - {(l_{1} l_{2} + m_{1} m_{2} + n_{1} n_{2})}^{2} \\ = {(m_{1} n_{2} - m_{2} n_{1})}^{2} + {(n_{1} l_{2} - n_{2} l_{1})}^{2} + {(l_{1} m_{2} - l_{2} m_{1})}^{2} \\ F r o m, (1), (2) & (3), w e . o b t a i n \\ \Rightarrow 1.1 - 0 = {(m_{1} n_{2} - m_{2} n_{1})}^{2} + {(n_{1} l_{2} - n_{2} l_{1})}^{2} + {(l_{1} m_{2} - l_{2} m_{1})}^{2} \\ ∴ {(m_{1} n_{2} - m_{2} n_{1})}^{2} + {(n_{1} l_{2} - n_{2} l_{1})}^{2} + {(l_{1} m_{2} - l_{2} m_{1})}^{2} = 1 . . . . . . . . . . (6) \end{array}$

Substituting the values from equations (5) and (6) in equation (4), we obtain

$\frac{l^{2}}{{(m_{1} n_{2} - m_{2} n_{1})}^{2}} = \frac{m^{2}}{{(n_{1} l_{2} - n_{2} l_{1})}^{2}} = \frac{n^{2}}{{(l_{1} m_{2} - l_{2} m_{1})}^{2}} = 1$

Thus, the direction cosines of the required line are $m_{1} n_{2} - m_{2} n_{1}, n_{1} l_{2} - n_{2} l_{1}, l_{1} m_{2} - l_{2} m_{1}$

0 Upvotes 0 Downvotes

Similar Questions for you

If $\int_{}^{} (\frac{x^{2} c o s x}{1 + π^{x}} + \frac{1 + s i n^{2} x}{1 + e^{{(s i n x)}^{2023}}}) d x = \frac{π}{4} (π + α) - 2$

Then the value of 'α' is equal to

alok kumar singh

$\int_{- \frac{π}{2}}^{\frac{π}{2}} (\frac{x^{2} c o s x}{1 + π^{2}} + \frac{1 + s i n^{2} x}{1 + e^{{(s i n x)}^{2023}}}) d x = \frac{π}{4} (π + α) - 2$

$\int_{0}^{\frac{π}{2}} {(\frac{x^{2} c o s x}{1 + π^{x}} + \frac{1 + s i n^{2} x}{1 + e^{{(s i n x)}^{2023}}}) + (\frac{x^{2} c o s x}{1 + π^{- x}} + \frac{1 + s i n^{2} x}{1 + e^{- {(s i n x)}^{2023}}})} d x$

$= \frac{π}{4} (π + α) - 2$

$\int_{0}^{\frac{π}{2}} (x^{2} c o s x + 1 + s i n^{2} x) d x = \frac{π}{4} (π + α) - 2$

$\int_{0}^{\frac{π}{2}} x^{2} c o s x d x + \int_{0}^{\frac{π}{2}} (1 + s i n^{2} x) d x = \frac{π}{4} (π + α) - 2$ ....(1)

Let $I_{1} = \int_{0}^{\frac{π}{2}} (1 + s i n^{2} x) d x$

$I_{1} = \int_{0}^{\frac{π}{2}} 1 \cdot d x + \int_{0}^{\frac{π}{2}} (\frac{1 - c o s 2 x}{2}) d x$

$I_{1} = \frac{π}{2} + \frac{1}{2} [\frac{π}{2} + 0]$

$I_{1} = \frac{3 π}{4}$

Let $I_{2} = \int_{0}^{\frac{π}{2}} x^{2} c o s x d x$

$I_{2} = {[x^{2} (s i n x) - \int 2 x \int c o s x d x]}_{0}^{\frac{π}{2}}$

$I_{2} = {[x^{2} (s i n x) - 2 \int x s i n x]}_{0}^{\frac{π}{2}}$

$I_{2} = {[x^{2} s i n x - 2 (x (- c o s x) + \int c o s x)]}_{0}^{\frac{π}{2}}$

$I_{2} = {[x^{2} s i n x - 2 (- x c o s x + s i n x)]}_{0}^{\frac{π}{2}}$

$I_{2} = (\frac{π^{2}}{4} - 2)$

Put l₁ and l₂ in (1)

$\frac{π^{2}}{4} - 2 + \frac{3 π}{4}$

$\frac{π^{2}}{4} + \frac{3 π}{4} - 2$

$\frac{π}{4} (π + 3) - 2$

α = 3

If $| \vec{a} | = 1$ , $| \vec{b} | = 4$ $\vec{a} \cdot \vec{b} = 2$ and $\vec{c} = 2 (\vec{a} \times \vec{b}) - 3 \vec{b}$ Then the angle between $\vec{b}$ and $\vec{c}$ is

alok kumar singh

Given $| \vec{a} | = 1$ , $| \vec{b} | = 4$ , $\vec{a} \cdot \vec{b} = 2$

$\vec{c} = 2 (\vec{a} \times \vec{b}) - 3 \vec{b}$

Dot product with $\vec{a}$ on both sides

$\vec{c} \cdot \vec{a} = - 6$ ... (1)

Dot product with $\vec{b}$ on both sides

$\vec{b} \cdot \vec{c} = - 48$ ... (2)

$\vec{c} \cdot \vec{c} = 4 {| \vec{a} \times \vec{b} |}^{2} + 9 {| \vec{b} |}^{2}$

${| \vec{c} |}^{2} = 4 [{| \vec{a} |}^{2} \cdot {| \vec{b} |}^{2} - {(\vec{a} \cdot \vec{b})}^{2}] + 9 {| \vec{b} |}^{2}$

${| \vec{c} |}^{2} = 4 [(1) {(4)}^{2} - (4)] + 9 (16)$

${| \vec{c} |}^{2} = 4 [12] + 144$

${| \vec{c} |}^{2} = 48 + 144$

${| \vec{c} |}^{2} = 192$

$c o s θ = \frac{\vec{b} \cdot \vec{c}}{| \vec{b} | | \vec{c} |}$

$c o s θ = \frac{- 48}{\sqrt[]{192} \cdot 4}$

$c o s θ = \frac{- 48}{8 \sqrt[]{3} \cdot 4}$

$c o s θ = \frac{- 3}{2 \sqrt[]{3}}$

$c o s θ = \frac{- \sqrt[]{3}}{2}$ $θ = c o s^{- 1} (\frac{- \sqrt[]{3}}{2})$

If the foot of perpendicular from (1, 2, 3) to the line $\frac{x + 1}{2} = \frac{y - 2}{5} = \frac{z - 4}{1}$ is (a, b, g) then find a + b + g

alok kumar singh

(a – 1) × 2 + (b – 2) × 5 + (g – 3) × 1 = 0

2a + 5b + g – 15 = 0

Also, P lie on line

a + 1 = 2λ

b – 2 = 5λ

g – 4 = λ

2 (2λ – 1) + 5 (5λ + 2) + λ + 4 – 15 = 0

4λ + 25λ + λ – 2 + 10 + 4 – 15 = 0

30λ – 3 = 0

$λ = \frac{1}{10}$

a + b + g = (2λ – 1) + (5λ + 2) + (λ + 4)

$= 8 λ + 5 = \frac{8}{10} + 5 = 5.8$

If (α, β, γ) is mirror image of the point (2, 3, 4) with respect to the line $\frac{x - 1}{2} = \frac{y - 2}{3} = \frac{z - 3}{4}$ Then 2α + 3β + 4γ is

alok kumar singh

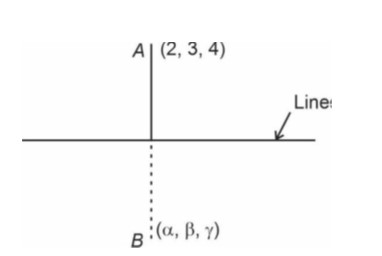
Take $\frac{x - 1}{2} = \frac{y - 2}{3} = \frac{z - 3}{4} = λ$

x = 2λ + 1, y = 3λ + 2, z = 4λ + 3

$\vec{A B}$ = (α − 2) $\hat{i}$ + (β − 3) $\hat{j}$ + (γ − 4) $\hat{k}$

Now,

(α − 2) ⋅ 2 + (β − 3) ⋅3 + (γ − 4) ⋅ 4 = 0

2α − 4 + 3β − 9 + 4γ −16 = 0

⇒ 2α + 3β + 4γ = 29

Let $λ$ be an integer. IF the shortest distance between the lines $x - λ = 2 y - 1 = - 2 z$ and $x = y + 2 λ = z - λ i s \frac{\sqrt[]{7}}{2 \sqrt[]{2}}$ , then the value of $| λ | i s . . . . . . . . . . . . . . . . . . .$

Vishal Baghel

$L_{1} = \frac{x - λ}{1} = \frac{y - \frac{1}{2}}{\frac{1}{2}} = \frac{z}{- \frac{1}{2}}$

$∴ S D = \frac{| - 2 λ + 3 (2 λ + \frac{1}{2}) + λ |}{\sqrt[]{14}} = \frac{| 5 λ + \frac{3}{2} |}{\sqrt[]{14}}$

$5 λ + \frac{3}{2} = - \frac{7}{2} \Rightarrow 5 λ = - 5 \Rightarrow λ = - 1$

$∴ | λ | = 1$

Get authentic answers from experts, students and alumni that you won't find anywhere else

On Shiksha, get access to

65k Colleges
1.2k Exams
688k Reviews
1800k Answers

Community GuidelinesUser Points System

QuestionsDiscussionsTags

39. If $l_{1}, m_{1}, n_{1} a n d l_{2}, m_{2}, n_{2}$ are the direction cosines of two mutually perpendicular lines, show that the direction cosines of the line perpendicular to both of these are $m_{1} n_{2} - m_{2} n_{1}, n_{1} l_{2} - n_{2} l_{1}, l_{1} m_{2} - l_{2} m_{1} .$

1 Answer

Similar Questions for you

Learn more about...

Most viewed information

Share Your College Life Experience

Didn't find the answer you were looking for?

Need guidance on career and education? Ask our experts

Your Question

39. If l1, m1, n1 and l2, m2, n2 are the direction cosines of two mutually perpendicular lines, show that the direction cosines of the line perpendicular to both of these are m1n2 − m2n1, n1l2 − n2l1, l1m2 ­− l2m1.

1 Answer

Similar Questions for you

Learn more about...

Most viewed information

Share Your College Life Experience

Didn't find the answer you were looking for?

Need guidance on career and education? Ask our experts

Your Question

39. If $l_{1}, m_{1}, n_{1} a n d l_{2}, m_{2}, n_{2}$ are the direction cosines of two mutually perpendicular lines, show that the direction cosines of the line perpendicular to both of these are $m_{1} n_{2} - m_{2} n_{1}, n_{1} l_{2} - n_{2} l_{1}, l_{1} m_{2} - l_{2} m_{1} .$