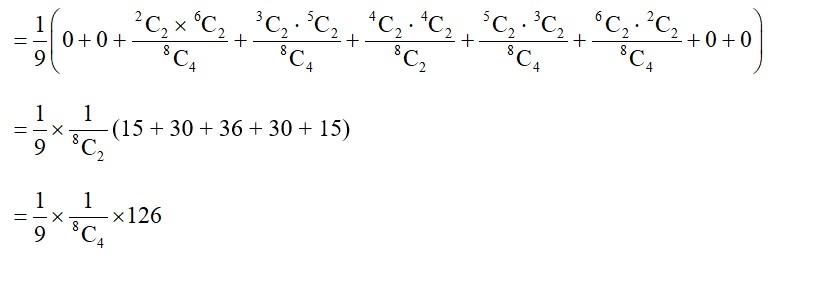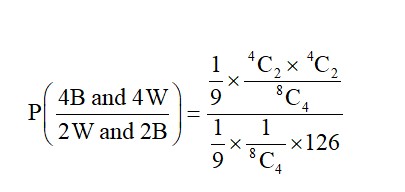53. Find the probability distribution of the number of success in two tosses of a die where a success is defined as:
(i) Number greater than 4.
(ii) Six appears on at least one die.
53. Find the probability distribution of the number of success in two tosses of a die where a success is defined as:
(i) Number greater than 4.
(ii) Six appears on at least one die.
53. When a die is tossed two times, we obtain (6 * 6) = 36 number of observations.
Let X be the random variable, which represents the number of successes.
(i) Here, success refers to the number greater than 4.
P (X = 0) = P (number less than or equal to 4 on both the tosses) = 4/6 X 4/6 = 4/9
P (X = 1)
Similar Questions for you
P (2 obtained on even numbered toss) = k (let)
P (2) =
P (
If x = 0, y = 6, 7, 8, 9, 10
If x = 1, y = 7, 8, 9, 10
If x = 2, y = 8, 9, 10
If x = 3, y = 9, 10
If x = 4, y = 10
If x = 5, y = no possible value
Total possible ways = (5 + 4 + 3 + 2 + 1) * 2
= 30
Required probability
P (2W and 2B) = P (2B, 6W) × P (2W and 2B)
+ P (3B, 5W) × P (2W and 2B)
+ P (4B, 4W) × P (2W and 2B)
+ P (5B, 3W) × P (2W and 2B)
+ P (6B, 2W) × P (2W and 2B)
(15 + 30 + 36 + 30 + 15)
Let probability of tail is
⇒ Probability of getting head =
∴ Probability of getting 2 heads and 1 tail
ax2 + bx + c = 0
D = b2 – 4ac
D = 0
b2 – 4ac = 0
b2 = 4ac
(i) AC = 1, b = 2 (1, 2, 1) is one way
(ii) AC = 4, b = 4
(iii) AC = 9, b = 6, a = 3, c = 3 is one way
1 + 3 + 1 = 5 way
Required probability =
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else.
On Shiksha, get access to
Learn more about...
Didn't find the answer you were looking for?
Search from Shiksha's 1 lakh+ Topics
Ask Current Students, Alumni & our Experts
Have a question related to your career & education?
See what others like you are asking & answering