Ncert Solutions Maths class 12th Maths Class 12th Three Dimensional Geometry

56. Find the vector equation of the line passing through the point (1, 2, − 4) and perpendicular to the two lines:

$\frac{x - 8}{3} = \frac{y + 19}{- 16} = \frac{z - 10}{7}$ and $\frac{x - 15}{3} = \frac{y - 29}{8} = \frac{z - 5}{- 5}$

38 Views | Posted 4 months ago

1 Answer

Answered by

Vishal Baghel | Contributor-Level 10

4 months ago

Let the required line be parallel to the vector $\vec{b}$ given by, $\vec{b} = b_{1} \hat{i} + b_{2} \hat{j} + b_{3} \hat{k}$

The position vector of the point (1, 2, − 4) is $\vec{a} = \hat{i} + 2 \hat{j} - 4 \hat{k}$

The equation of the line passing through (1, 2, −4) and parallel to vector $\vec{b}$ is

$\begin{array}{l} \vec{r} = \vec{a} + λ \vec{b} \\ \Rightarrow \vec{r} = (\hat{i} + 2 \hat{j} - 4 \hat{k}) + λ (b_{1} \hat{i} + b_{2} \hat{j} + b_{3} \hat{k}) . . . . . . . (1) \end{array}$

The equations of the lines are

$\begin{array}{l} \frac{x - 8}{3} = \frac{y + 19}{- 16} = \frac{z - 10}{7} . . . . . . . . (2) \\ \frac{x - 15}{3} = \frac{y - 29}{8} = \frac{z - 5}{- 5} . . . . . . . . (3) \end{array}$

Line (1) and line (2) are perpendicular to each other.

$∴ 3 b_{1} - 16 b_{2} + 7 b_{3} = 0 . . . . . . . . (4)$

Also, line (1) and line (3) are perpendicular to each other.

$∴ 3 b_{1} + 8 b_{2} - 5 b_{3} = 0 . . . . . . . . (5)$

From equations (4) and (5), we obtain

$\begin{array}{l} \frac{b_{1}}{(- 16) (- 5) - 8 \times 7} = \frac{b_{2}}{7 \times 3 - 3 (- 5)} = \frac{b_{3}}{3 \times 8 - 3 (- 16)} \\ \Rightarrow \frac{b_{1}}{24} = \frac{b_{2}}{36} = \frac{b_{3}}{72} \\ \Rightarrow \frac{b_{1}}{2} = \frac{b_{2}}{3} = \frac{b_{3}}{6} \end{array}$

Direction ratios of $\vec{b}$ are 2, 3, and 6.

$∴ \vec{b} = 2 \hat{i} + 3 \hat{j} + 6 \hat{k}$

Substituting $\vec{b} = 2 \hat{i} + 3 \hat{j} + 6 \hat{k}$ in equation (1), we obtain

$\vec{r} = (\hat{i} + 2 \hat{j} - 4 \hat{k}) + λ (2 \hat{i} + 3 \hat{j} + 6 \hat{k})$

This is the equation of the required line.

0 Upvotes 0 Downvotes

Similar Questions for you

If $\int_{}^{} (\frac{x^{2} c o s x}{1 + π^{x}} + \frac{1 + s i n^{2} x}{1 + e^{{(s i n x)}^{2023}}}) d x = \frac{π}{4} (π + α) - 2$

Then the value of 'α' is equal to

alok kumar singh

$\int_{- \frac{π}{2}}^{\frac{π}{2}} (\frac{x^{2} c o s x}{1 + π^{2}} + \frac{1 + s i n^{2} x}{1 + e^{{(s i n x)}^{2023}}}) d x = \frac{π}{4} (π + α) - 2$

$\int_{0}^{\frac{π}{2}} {(\frac{x^{2} c o s x}{1 + π^{x}} + \frac{1 + s i n^{2} x}{1 + e^{{(s i n x)}^{2023}}}) + (\frac{x^{2} c o s x}{1 + π^{- x}} + \frac{1 + s i n^{2} x}{1 + e^{- {(s i n x)}^{2023}}})} d x$

$= \frac{π}{4} (π + α) - 2$

$\int_{0}^{\frac{π}{2}} (x^{2} c o s x + 1 + s i n^{2} x) d x = \frac{π}{4} (π + α) - 2$

$\int_{0}^{\frac{π}{2}} x^{2} c o s x d x + \int_{0}^{\frac{π}{2}} (1 + s i n^{2} x) d x = \frac{π}{4} (π + α) - 2$ ....(1)

Let $I_{1} = \int_{0}^{\frac{π}{2}} (1 + s i n^{2} x) d x$

$I_{1} = \int_{0}^{\frac{π}{2}} 1 \cdot d x + \int_{0}^{\frac{π}{2}} (\frac{1 - c o s 2 x}{2}) d x$

$I_{1} = \frac{π}{2} + \frac{1}{2} [\frac{π}{2} + 0]$

$I_{1} = \frac{3 π}{4}$

Let $I_{2} = \int_{0}^{\frac{π}{2}} x^{2} c o s x d x$

$I_{2} = {[x^{2} (s i n x) - \int 2 x \int c o s x d x]}_{0}^{\frac{π}{2}}$

$I_{2} = {[x^{2} (s i n x) - 2 \int x s i n x]}_{0}^{\frac{π}{2}}$

$I_{2} = {[x^{2} s i n x - 2 (x (- c o s x) + \int c o s x)]}_{0}^{\frac{π}{2}}$

$I_{2} = {[x^{2} s i n x - 2 (- x c o s x + s i n x)]}_{0}^{\frac{π}{2}}$

$I_{2} = (\frac{π^{2}}{4} - 2)$

Put l₁ and l₂ in (1)

$\frac{π^{2}}{4} - 2 + \frac{3 π}{4}$

$\frac{π^{2}}{4} + \frac{3 π}{4} - 2$

$\frac{π}{4} (π + 3) - 2$

α = 3

If $| \vec{a} | = 1$ , $| \vec{b} | = 4$ $\vec{a} \cdot \vec{b} = 2$ and $\vec{c} = 2 (\vec{a} \times \vec{b}) - 3 \vec{b}$ Then the angle between $\vec{b}$ and $\vec{c}$ is

alok kumar singh

Given $| \vec{a} | = 1$ , $| \vec{b} | = 4$ , $\vec{a} \cdot \vec{b} = 2$

$\vec{c} = 2 (\vec{a} \times \vec{b}) - 3 \vec{b}$

Dot product with $\vec{a}$ on both sides

$\vec{c} \cdot \vec{a} = - 6$ ... (1)

Dot product with $\vec{b}$ on both sides

$\vec{b} \cdot \vec{c} = - 48$ ... (2)

$\vec{c} \cdot \vec{c} = 4 {| \vec{a} \times \vec{b} |}^{2} + 9 {| \vec{b} |}^{2}$

${| \vec{c} |}^{2} = 4 [{| \vec{a} |}^{2} \cdot {| \vec{b} |}^{2} - {(\vec{a} \cdot \vec{b})}^{2}] + 9 {| \vec{b} |}^{2}$

${| \vec{c} |}^{2} = 4 [(1) {(4)}^{2} - (4)] + 9 (16)$

${| \vec{c} |}^{2} = 4 [12] + 144$

${| \vec{c} |}^{2} = 48 + 144$

${| \vec{c} |}^{2} = 192$

$c o s θ = \frac{\vec{b} \cdot \vec{c}}{| \vec{b} | | \vec{c} |}$

$c o s θ = \frac{- 48}{\sqrt[]{192} \cdot 4}$

$c o s θ = \frac{- 48}{8 \sqrt[]{3} \cdot 4}$

$c o s θ = \frac{- 3}{2 \sqrt[]{3}}$

$c o s θ = \frac{- \sqrt[]{3}}{2}$ $θ = c o s^{- 1} (\frac{- \sqrt[]{3}}{2})$

If the foot of perpendicular from (1, 2, 3) to the line $\frac{x + 1}{2} = \frac{y - 2}{5} = \frac{z - 4}{1}$ is (a, b, g) then find a + b + g

alok kumar singh

(a – 1) × 2 + (b – 2) × 5 + (g – 3) × 1 = 0

2a + 5b + g – 15 = 0

Also, P lie on line

a + 1 = 2λ

b – 2 = 5λ

g – 4 = λ

2 (2λ – 1) + 5 (5λ + 2) + λ + 4 – 15 = 0

4λ + 25λ + λ – 2 + 10 + 4 – 15 = 0

30λ – 3 = 0

$λ = \frac{1}{10}$

a + b + g = (2λ – 1) + (5λ + 2) + (λ + 4)

$= 8 λ + 5 = \frac{8}{10} + 5 = 5.8$

If (α, β, γ) is mirror image of the point (2, 3, 4) with respect to the line $\frac{x - 1}{2} = \frac{y - 2}{3} = \frac{z - 3}{4}$ Then 2α + 3β + 4γ is

alok kumar singh

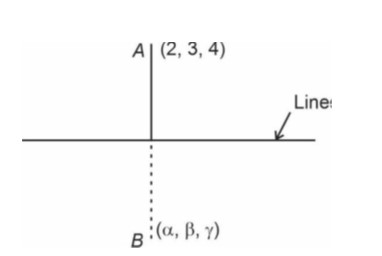
Take $\frac{x - 1}{2} = \frac{y - 2}{3} = \frac{z - 3}{4} = λ$

x = 2λ + 1, y = 3λ + 2, z = 4λ + 3

$\vec{A B}$ = (α − 2) $\hat{i}$ + (β − 3) $\hat{j}$ + (γ − 4) $\hat{k}$

Now,

(α − 2) ⋅ 2 + (β − 3) ⋅3 + (γ − 4) ⋅ 4 = 0

2α − 4 + 3β − 9 + 4γ −16 = 0

⇒ 2α + 3β + 4γ = 29

Let $λ$ be an integer. IF the shortest distance between the lines $x - λ = 2 y - 1 = - 2 z$ and $x = y + 2 λ = z - λ i s \frac{\sqrt[]{7}}{2 \sqrt[]{2}}$ , then the value of $| λ | i s . . . . . . . . . . . . . . . . . . .$

Vishal Baghel

$L_{1} = \frac{x - λ}{1} = \frac{y - \frac{1}{2}}{\frac{1}{2}} = \frac{z}{- \frac{1}{2}}$

$∴ S D = \frac{| - 2 λ + 3 (2 λ + \frac{1}{2}) + λ |}{\sqrt[]{14}} = \frac{| 5 λ + \frac{3}{2} |}{\sqrt[]{14}}$

$5 λ + \frac{3}{2} = - \frac{7}{2} \Rightarrow 5 λ = - 5 \Rightarrow λ = - 1$

$∴ | λ | = 1$

Get authentic answers from experts, students and alumni that you won't find anywhere else

On Shiksha, get access to

65k Colleges
1.2k Exams
688k Reviews
1800k Answers

Community GuidelinesUser Points System

QuestionsDiscussionsTags

56. Find the vector equation of the line passing through the point (1, 2, − 4) and perpendicular to the two lines:

$\frac{x - 8}{3} = \frac{y + 19}{- 16} = \frac{z - 10}{7}$ and $\frac{x - 15}{3} = \frac{y - 29}{8} = \frac{z - 5}{- 5}$

1 Answer

Similar Questions for you

Learn more about...

Most viewed information

Share Your College Life Experience

Didn't find the answer you were looking for?

Need guidance on career and education? Ask our experts

Your Question

56. Find the vector equation of the line passing through the point (1, 2, − 4) and perpendicular to the two lines: x−83=y+19−16=z−107 and x−153=y−298=z−5−5

1 Answer

Similar Questions for you

Learn more about...

Most viewed information

Share Your College Life Experience

Didn't find the answer you were looking for?

Need guidance on career and education? Ask our experts

Your Question

56. Find the vector equation of the line passing through the point (1, 2, − 4) and perpendicular to the two lines:

$\frac{x - 8}{3} = \frac{y + 19}{- 16} = \frac{z - 10}{7}$ and $\frac{x - 15}{3} = \frac{y - 29}{8} = \frac{z - 5}{- 5}$