7. Find the angle in radian through which a pendulum swings if its length is 75 cm and the tip describes an arc of length
(i) 10 cm (ii) 15 cm (iii) 21 cm
7. Find the angle in radian through which a pendulum swings if its length is 75 cm and the tip describes an arc of length
(i) 10 cm (ii) 15 cm (iii) 21 cm
-
1 Answer
-
7. Here,
r= length of pendulum.
r= 75 cm.
(i) Arc of length, l = 10 cm
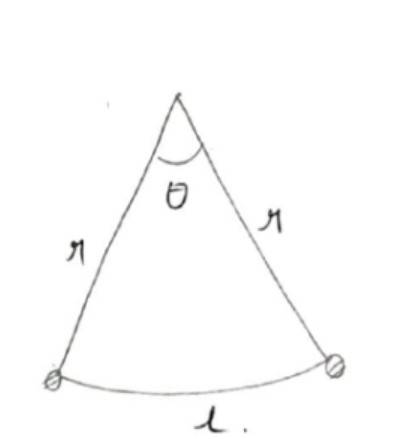
Ø= = radian.
(ii) Arc of length, l = 15 cm.
So, Ø= = radian.
(iii) Arc for length, l= 21 cm.
So, Ø= radian.
Similar Questions for you
16cos2θ + 25sin2θ + 40sinθ cosθ = 1
16 + 9sin2θ + 20sin 2θ = 1
+ 20sin 2θ = 1
– 9cos 2θ + 40sin 2θ = – 39
48tan2θ + 80tanθ + 30 = 0
24tan2θ + 40tanθ + 15 = 0
-> ,
So will be rejected as
Option (4) is correct.
12x =
is the solution of above equation.
Statement 1 is true
f(0) = – 1 < 0
one root lies in , one root is which is positive. As the coefficients are real, therefore all the roots must be real.
Statement 2 is false.
tan2 A = tan B tan C
It is only possible when A = B = C at x = 1
A = 30°, B = 30°, C = 30°
a = sin−1 (sin5) = 5 − 2π
and b = cos−1 (cos5) = 2π − 5
∴ a2 + b2 = (5 − 2π)2 + (2π − 5)2
= 8π2 − 40π + 50
sin 2 + tan 2 > 0
Let tan = x
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers
