A square with maximum possible length of the side is inscribed in an equilateral triangle and a circle of maximum possible radius is inscribed in the square. Find the ratio of the length of equilateral of the equilateral triangle to the radius of circle.

Correct Option - 3


Detailed Solution: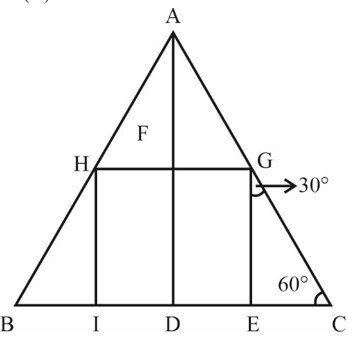

Let the side of = a

CD = a/2

Let EC = x

In GEC

GE/EC = tan60 = $\sqrt[]{3}$

GE = x $\sqrt[]{3}$

DE = a/2 – x = FG = HF

GE = HG

$x\sqrt[]{3}=\frac{a}{2}-x+\frac{a}{2}-x$

x $\sqrt[]{3}$ = a – 2x

x = $\frac{a}{\sqrt[]{3}+2}$

GE = x $\sqrt[]{3}$ = $\frac{a\sqrt[]{3}}{\sqrt[]{3}+2}$

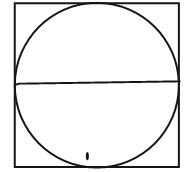
r = side of square ÷ 2

r= $\frac{a\sqrt[]{3}}{4+2\sqrt[]{3}}$

ratio = a/r

= $\frac{a(4+2\sqrt[]{3})}{a\sqrt[]{3}}$

= $\frac{4+2\sqrt[]{3})}{\sqrt[]{3}}=\frac{4}{\sqrt[]{3}}+2$

<div><picture><img src="https://images.shiksha.com/mediadata/images/1754906456phpusD1NV.jpeg" alt="" width="119" height="113" loading="lazy"></picture></div><div><p>Let the side of = a</p><p>CD = a/2</p><p>Let EC = x</p><p>In GEC</p><p>GE/EC = tan60 =&nbsp;<math><mrow><mroot><mrow><mn>3</mn></mrow><mrow></mrow></mroot></mrow></math></p><p>GE = x&nbsp;<math><mrow><mroot><mrow><mn>3</mn></mrow><mrow></mrow></mroot></mrow></math></p><p>DE = a/2 – x = FG = HF</p><p>GE = HG</p><p><math><mrow><mi>x</mi><mroot><mrow><mn>3</mn></mrow><mrow></mrow></mroot><mo>=</mo><mfrac><mrow><mi>a</mi></mrow><mrow><mn>2</mn></mrow></mfrac><mo>−</mo><mi>x</mi><mo>+</mo><mfrac><mrow><mi>a</mi></mrow><mrow><mn>2</mn></mrow></mfrac><mo>−</mo><mi>x</mi></mrow></math></p><p>x&nbsp;<math><mrow><mroot><mrow><mn>3</mn></mrow><mrow></mrow></mroot></mrow></math>&nbsp;= a – 2x</p><p>x =&nbsp;<math><mrow><mfrac><mrow><mi>a</mi></mrow><mrow><mroot><mrow><mn>3</mn></mrow><mrow></mrow></mroot><mo>+</mo><mn>2</mn></mrow></mfrac></mrow></math></p><p>GE = x&nbsp;<math><mrow><mroot><mrow><mn>3</mn></mrow><mrow></mrow></mroot></mrow></math>&nbsp;=&nbsp;<math><mrow><mfrac><mrow><mi>a</mi><mroot><mrow><mn>3</mn></mrow><mrow></mrow></mroot></mrow><mrow><mroot><mrow><mn>3</mn></mrow><mrow></mrow></mroot><mo>+</mo><mn>2</mn></mrow></mfrac></mrow></math></p><div><div><picture><source srcset="" media=" (max-width: 500px)"><img src="https://images.shiksha.com/mediadata/images/1754906520phpx9fMgh.jpeg" alt="" width="88" height="78" loading="lazy"></picture></div></div><p>r = side of square ÷ 2</p><p>r=&nbsp;<math><mrow><mfrac><mrow><mi>a</mi><mroot><mrow><mn>3</mn></mrow><mrow></mrow></mroot></mrow><mrow><mn>4</mn><mo>+</mo><mn>2</mn><mroot><mrow><mn>3</mn></mrow><mrow></mrow></mroot></mrow></mfrac></mrow></math></p><p>ratio = a/r</p><p>=&nbsp;<math><mrow><mfrac><mrow><mi>a</mi><mo stretchy="false"> (</mo><mn>4</mn><mo>+</mo><mn>2</mn><mroot><mrow><mn>3</mn></mrow><mrow></mrow></mroot><mo stretchy="false">)</mo></mrow><mrow><mi>a</mi><mroot><mrow><mn>3</mn></mrow><mrow></mrow></mroot></mrow></mfrac></mrow></math></p><p>=&nbsp;<math><mrow><mfrac><mrow><mn>4</mn><mo>+</mo><mn>2</mn><mroot><mrow><mn>3</mn></mrow><mrow></mrow></mroot><mo stretchy="false">)</mo></mrow><mrow><mroot><mrow><mn>3</mn></mrow><mrow></mrow></mroot></mrow></mfrac><mo>=</mo><mfrac><mrow><mn>4</mn></mrow><mrow><mroot><mrow><mn>3</mn></mrow><mrow></mrow></mroot></mrow></mfrac><mo>+</mo><mn>2</mn></mrow></math></p></div>

0 Upvotes 0 Upvotes 0 Downvotes

• • Report Abuse
• Comment