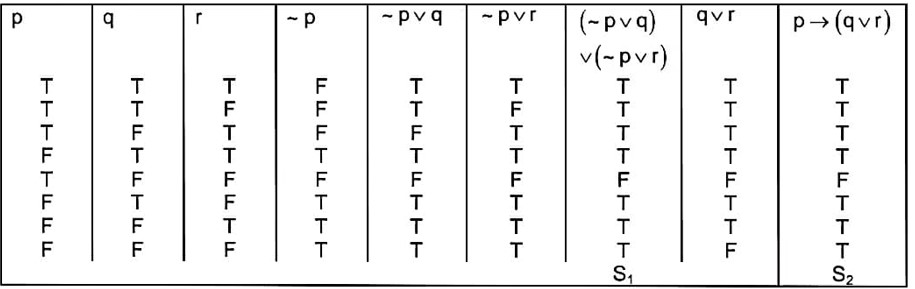
Given the following two statements:
(S₁): (q∨p) → (p ↔~ q) is a tautology.
(S₂): ~ q∧ (~ p ↔ q) is a fallacy. Then:

pva $\left(\sim rvp\right)$ $$

$\sim \left(p\vee q\right)\vee \left(\sim rvp\right)$

its negation as asked in question

$\left(p\vee q\right)\wedge \left(\sim p\wedge r\right)$

= $\left(p\wedge \sim p\wedge r\right)\vee \left(q\wedge r\wedge \sim p\right)$

= $\left(p\wedge r\wedge \sim p\right)\left[asp\wedge \sim pisfalse\right]$

$2021\equiv -2$ mod (7)

$\Rightarrow {\left(2021\right)}^{2023}\equiv {\left(-2\right)}^{2023}mod\left(7\right)$   …… (i)

Now,   ${\left(-2\right)}^3\equiv -1mod\left(7\right)$  

$\Rightarrow {\left(-2\right)}^{2023}\equiv \left(-2\right)mod\left(7\right)\equiv 5mod\left(7\right)$       ……. (ii)

(i) & (ii)

$\Rightarrow {\left(2021\right)}^{2023}\equiv 5mod\left(7\right)$  

$\therefore$  Remainder = 5

kindly consider the following Image 

$\sim \left(p\iff \sim q\right)\wedge q=\left(p\iff \sim q\right)\wedge qis:$

$\therefore \left(\sim \left(P\iff \sim Q\right)\right)\wedge$ q is equivalent to $\left(p\Rightarrow q\right)\wedge$