(i) If and , then
(ii) If , then and .
(iii) If , then and .
(iv) If , then and .
(v) If and , then .
(vi) If and , then .
(vii) If and , then .
(viii) If , then
(ix) If , then
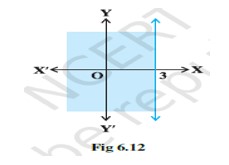
(x) Graph of corresponds to Fig 6.12.
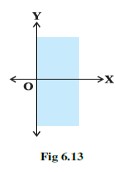
(xi) Graph of corresponds to Fig 6.13.
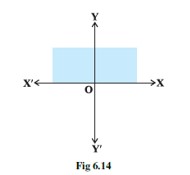
(xii) Graph of corresponds to Fig 6.14.
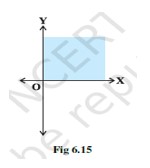
(xiii) Solution set of and corresponds to Fig 6.15.
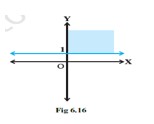
(xiv) Solution set of and corresponds to Fig 6.16.
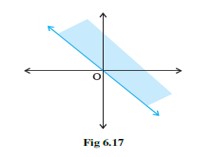
(xv) Solution set of corresponds to Fig 6.17.
(i) If and , then
(ii) If , then and .
(iii) If , then and .
(iv) If , then and .
(v) If and , then .
(vi) If and , then .
(vii) If and , then .
(viii) If , then
(ix) If , then
(x) Graph of corresponds to Fig 6.12.
(xi) Graph of corresponds to Fig 6.13.
(xii) Graph of corresponds to Fig 6.14.
(xiii) Solution set of and corresponds to Fig 6.15.
(xiv) Solution set of and corresponds to Fig 6.16.
(xv) Solution set of corresponds to Fig 6.17.
This is a True or False Type Questions as classified in NCERT Exemplar
Similar Questions for you
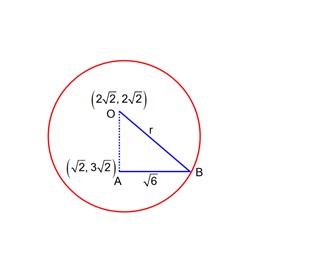
centre
radius
centre
OA =
r2 =
Let y = mx + c is the common tangent
so equation of common tangents will be
which intersects at Q (3, 0)
Major axis and minor axis of ellipse are 12 and 6. So eccentricity
and length of latus rectum
Hence
This is a Fill in the blanks Type Questions as classified in NCERT Exemplar
30.
30. For inequality y+8 ≤ 2x, the equation of the line is y+8=2x. We consider the table below to plot of y+8=2x.
The line devides the xy-plane into half planer I and II. We select a point (0,0) and check the correctness of the inequality.
i.e., 0+8 ≤ 2 × 0
0 ≤ 0 which is true.
So, the solu
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else.
On Shiksha, get access to
Learn more about...

Maths NCERT Exemplar Solutions Class 11th Chapter Six 2025
View Exam DetailsMost viewed information
SummaryDidn't find the answer you were looking for?
Search from Shiksha's 1 lakh+ Topics
Ask Current Students, Alumni & our Experts
Have a question related to your career & education?
See what others like you are asking & answering