LE the common tangents to the curves and y2 = 4x intersect at the point Q. Let an ellipse, centered at the origin O, has lengths of semi-minor and semi-major axes equal to OQ and 6, respectively. If e and respectively denote the eccentricity and the length of the latus rectum of this ellipse, then is equal to
LE the common tangents to the curves and y2 = 4x intersect at the point Q. Let an ellipse, centered at the origin O, has lengths of semi-minor and semi-major axes equal to OQ and 6, respectively. If e and respectively denote the eccentricity and the length of the latus rectum of this ellipse, then is equal to
-
1 Answer
-
Let y = mx + c is the common tangent
so equation of common tangents will be
which intersects at Q (3, 0)
Major axis and minor axis of ellipse are 12 and 6. So eccentricity
and length of latus rectum
Hence
Similar Questions for you
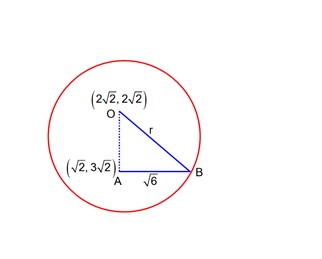
centre
radius
centre
OA =
r2 =
This is a Fill in the blanks Type Questions as classified in NCERT Exemplar
This is a True or False Type Questions as classified in NCERT Exemplar
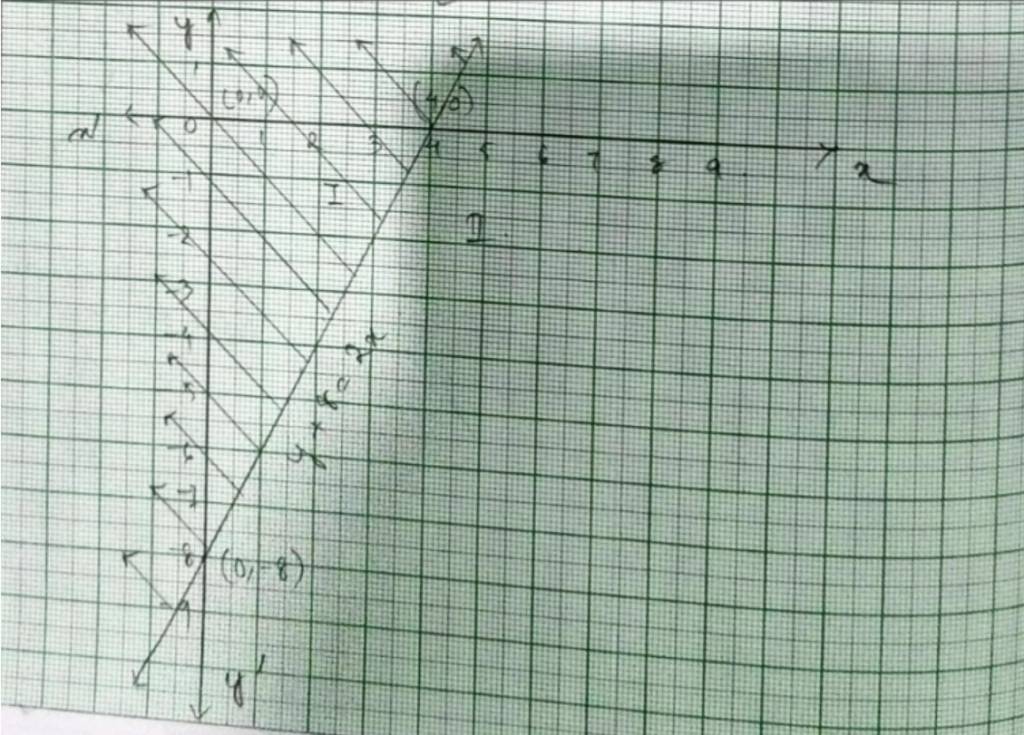
30.
30. For inequality y+8 ≤ 2x, the equation of the line is y+8=2x. We consider the table below to plot of y+8=2x.
The line devides the xy-plane into half planer I and II. We select a point (0,0) and check the correctness of the inequality.
i.e., 0+8 ≤ 2 × 0
0 ≤ 0 which is true.
So, the solution region is I which includes the rigin (0,0). The continuous line also indicates that any points on the line also satisfy the given inequality.
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers