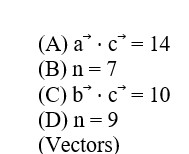Search Colleges, Courses, Exams, Questions and Articles

Ask a query on 8879100846 Ask Login | Sign Up

 

 

› Ask & Answer › Question

If the volume of a parallelepiped, whose coterminus edges are given by the vectors a⃗ = î + ĵ + nk̂, b⃗ = 2î + 4ĵ – nk̂ and c⃗ = î + nĵ + 3k̂(n ≥ 0), is 158 cu.units. then:

 


Option 1 -

A

Option 2 -

B

Option 3 -

C

Option 4 -

D

0 3 Views | Posted a month ago
Asked by Shiksha User

  • 1 Answer

  • A

    Answered by

    alok kumar singh | Contributor-Level 10

    a month ago
    Correct Option - 3


    Detailed Solution:

    Volume of parallelepiped v = | [a? b? c? ]|
    v = | 1 n |
    | 2 4 -n| = ±158
    | 1 n 3 |
    1 (12+n²) - 1 (6+n) + n (2n-4) = ±158
    3n²-5n+152=0 or 3n²-5n+164=0
    D<0 (no real roots)
    n=8, -19/3 ⇒ n=8
    then b? ⋅c? = 2+4n-3n=10
    a? ⋅c? = 1+n+3n=33

Get authentic answers from experts, students and alumni that you won't find anywhere else

Sign Up on Shiksha

On Shiksha, get access to

  • 65k Colleges
  • 1.2k Exams
  • 688k Reviews
  • 1800k Answers

Learn more about...

Share Your College Life Experience

Write a Review

Didn't find the answer you were looking for?

Search from Shiksha's 1 lakh+ Topics

or

Ask Current Students, Alumni & our Experts

Ask Now
Community GuidelinesUser Points System
QuestionsDiscussionsTags
×
×

This website uses Cookies and related technologies for the site to function correctly and securely, improve & personalise your browsing experience, analyse traffic, and support our marketing efforts and serve the Core Purpose. By continuing to browse the site, you agree to Privacy Policy and Cookie Policy.

Need guidance on career and education? Ask our experts

Characters 0/140

The Answer must contain atleast 20 characters.

Add more details

Characters 0/300

The Answer must contain atleast 20 characters.

Keep it short & simple. Type complete word. Avoid abusive language. Next

Your Question

Edit

Add relevant tags to get quick responses. Cancel Post