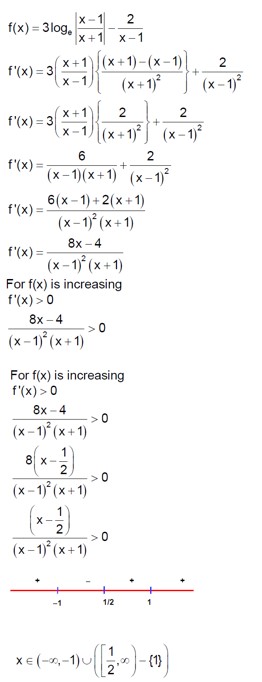Search Colleges, Courses, Exams, Questions and Articles

Ask a query on 8879100846 Ask Login | Sign Up

 

 

› Ask & Answer › Question

Let a line L1 be tangent to the hyperbola   x 2 1 6 − y 2 4 = 1  and let L2 be the line passing through the origin and perpendicular to L1. If the locus of the point of intersection of L1 and L2 is ( x 2 + y 2 ) 2 = αx2 + βy2, then α + β is equal to……….

0 2 Views | Posted 2 months ago
Asked by Shiksha User

  • 1 Answer

  • V

    Answered by

    Vishal Baghel | Contributor-Level 10

    2 months ago

    Equation of L1 = is

    x s e c θ 4 − y t a n θ 2 = 1 ….(i)

    Equation of line L2 is

    x t a n θ 2 + y s e c θ 4 = 0 ….(ii)

    ? Required point of intersection of L1 and L2 is (x1, y1) then

    x 1 s e c θ 4 − y 1 t a n θ 2 − 1 = 0 ….(iii)

    a n d     y 1 s e c θ 4 + x 1 t a n θ 2 = 0 ……(iv)

    From equations (iii) and (iv)

    s e c θ = 4 x 1 x 1 2 + y 1 2 a n d     t a n θ = − 2 y 1 x 1 2 + y 1 2        

    ∴ Required locus of (x1, y1) is

    ( x 2 + y 2 ) 2 = 1 6 x 2 − 4 y 2   

    ∴ α = 1 6 , β = − 4 ∴ α = β = 1 2     

Similar Questions for you

Let f and g be twice differentiable even functions on (-2, 2) such that f ( 1 4 ) = 0 ,     f ( 1 2 ) = 0 ,     f ( 1 ) = 1 and f ( 3 4 ) = 0 ,     g ( 1 ) = 2  

Then, the minimum number of solutions of f ( x ) g " ( x ) + f ' ( x ) g ' ( x ) = 0     i n     ( − 2 , 2 )  is equal to……….
V
Vishal Baghel

f (x) is an even function

f ( − 1 4 ) = f ( − 1 2 ) = f ( 1 2 ) = f ( 1 4 ) = 0  

So, f (x) has at least four roots in (-2, 2)

g ( − 3 4 ) = g ( 3 4 ) = 0         

So, g (x) has at least two roots in (-2, 2)

now number of roots of f (x) ⋅ g " ( x ) = f ' ( x ) ⋅ g ' ( x ) = 0  

It is same as number of roots of d d x ( f ( x ) ⋅ g ' ( x ) ) = 0 will have atleast 4 roots in (-2, 2)

Let f be a real valued continuous function on [0, 1] and f(x) = x + ∫ 0 1 ( x − t ) f ( t ) d t .  Then, which of the following points (x, y) lies on the curve y = f(x)?
V
Vishal Baghel

f ( x ) = x + x ∫ 0 1 f ( t ) d t − ∫ 0 1 t 0 f ( t ) d t

Let 1 + ∫ 0 1 f ( t ) d t = α

∫ 0 1 t     f ( t ) d t = β

So, f(x) = x

Now, α = ∫ 0 1 f ( t ) d t + 1

α = ∫ 0 1 ( a t − β ) d t + 1

β = ∫ 0 1 t ⋅ f ( t ) d t

β = 4 1 3 , α = 1 8 1 3

f(x) = αx – b

= 1 8 x − 4 1 3

option (D) satisfies

Let f(x) be non-constant thrice differentiable function defined on ( − ∞ ,     ∞ )  such that f(x) = f(6 – x) and f’(0) = 0 = f’(2) = f’(5). If ‘n’ is the minimum number of roots of (f”(x))2 + f(x)f”(x) = 0 in the interval x ∈  [0, 6] then sum of digits of n equals
V
Vishal Baghel

f (x) = f (6 – x) Þ f' (x) = -f' (6 – x) …. (1)

put x = 0, 2, 5

f' (0) = f' (6) = f' (2) = f' (4) = f' (5) = f' (1) = 0

and from equation (1) we get f' (3) = -f' (3)

? f ' ( 3 ) = 0

So f' (x) = 0 has minimum 7 roots in x ? [ 0 , 6 ] ? f ' ' ( x )  has min 6 roots in   x ? [ 0 , 6 ]

h (x) = f' (x) . f' (x)

h' (x) = (f' (x)2 + f' (x) f' (x)

h (x) = 0 has 13 roots in x ?   [0, 6]

h' (x) = 0 has 12 roots in x ? [0, 6]

If 1+x4-x5 = Σi=05 a?(1+x)i, for all x ∈ R, then a2 is equal to ____________
V
Vishal Baghel

1 + x? - x? = a? (1+x)? + a? (1+x) + a? (1+x)² . + a? (1+x)?
Differentiate
4x³ - 5x? = a? + 2a? (1+x) + 3a? (1+x)².
12x² - 20x³ = 2a? + 6a? (1+x).
Put x = -1
12 + 20 = 2a? ⇒ a? = 16

Let f be a real valued function, defined on R - {-1, 1} and given by f(x) = 3logₑ|(x-1)/(x+1)| - 2/(x-1). Then in which of the following intervals, function f(x) is increasing?
A
alok kumar singh

Kindly go through the solution 

 

Get authentic answers from experts, students and alumni that you won't find anywhere else

Sign Up on Shiksha

On Shiksha, get access to

  • 65k Colleges
  • 1.2k Exams
  • 688k Reviews
  • 1800k Answers

Learn more about...

Share Your College Life Experience

Write a Review

Didn't find the answer you were looking for?

Search from Shiksha's 1 lakh+ Topics

or

Ask Current Students, Alumni & our Experts

Ask Now
Community GuidelinesUser Points System
QuestionsDiscussionsTags
×

This website uses Cookies and related technologies for the site to function correctly and securely, improve & personalise your browsing experience, analyse traffic, and support our marketing efforts and serve the Core Purpose. By continuing to browse the site, you agree to Privacy Policy and Cookie Policy.

Need guidance on career and education? Ask our experts

Characters 0/140

The Answer must contain atleast 20 characters.

Add more details

Characters 0/300

The Answer must contain atleast 20 characters.

Keep it short & simple. Type complete word. Avoid abusive language. Next

Your Question

Edit

Add relevant tags to get quick responses. Cancel Post