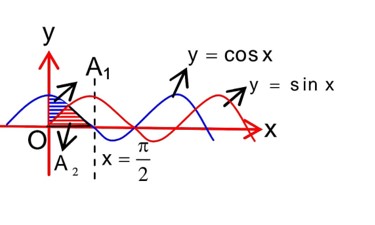
Let A₁ be the area of the region bounded by the curves y = sinx, y = cosx and y-axis in the first quadrant. Also, let A₂ be the area of the region bounded by the curves y = sinx, y = cosx, x-axis and x = $\frac{\pi }{2}$  in the first quadrant. Then,

$\left|x^2-9\right|=3$

$\Rightarrow x=\pm 2\sqrt[]{3},\pm \sqrt[]{6}$

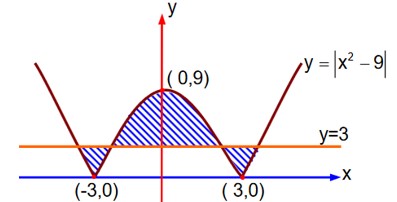
Required area = A

$\frac{A}{2}={\displaystyle \underset{0}{\overset{\sqrt[]{6}}{\int }}\left(9-x^2-3\right)dx+{\displaystyle \underset{0}{\overset{3}{\int }}\left(\sqrt[]{9+y}-\sqrt[]{9-y}\right)dy}}$

$A=16\sqrt[]{6}+32\sqrt[]{3}-72=8\left[2\sqrt[]{6}+4\sqrt[]{3}-9\right]$

Note : No option in the question paper is correct.

$y^2\le 8xy>\sqrt[]{2}x$

$2x^2=8x\Rightarrow x\left(x-4\right)=0\Rightarrow x=0,x=4x=0,x=y$

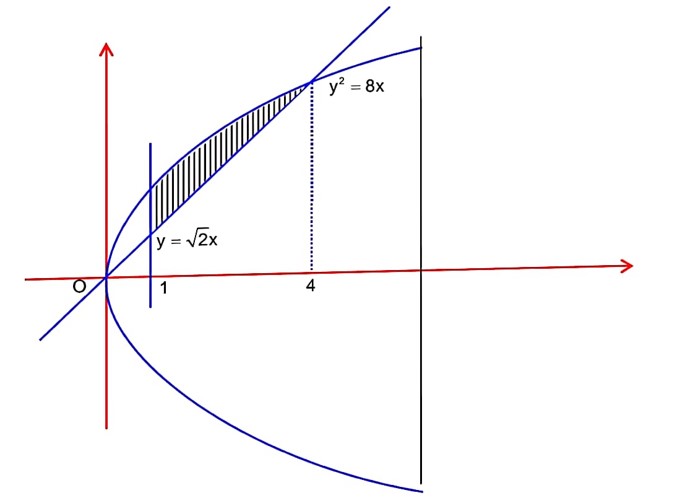
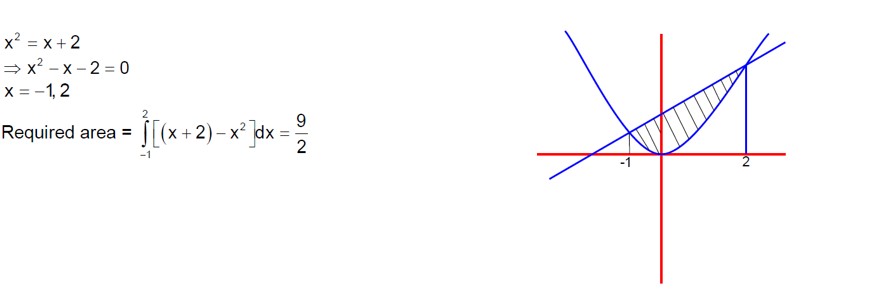
Required area = ${\displaystyle \underset{1}{\overset{4}{\int }}\left(2\sqrt[]{2}\sqrt[]{x}-\sqrt[]{2}x\right)}$ dx

$=\frac{28\sqrt[]{2}}{3}-\frac{15\sqrt[]{2}}{2}=\frac{11\sqrt[]{2}}{6}$

  $A\left(a\right)=2{\displaystyle \underset{0}{\overset{\sqrt[]{1-a}}{\int }}\left(\left(1-x^2\right)-a\right)dx=\frac{4}{3}{\left(1-a\right)}^{3/2}}$  

  $\therefore A\left(0\right)=\frac{4}{3}$            

and    ^{$A\left(\frac{1}{2}\right)=\frac{4}{3}{\left(\frac{1}{2}\right)}^{\frac{3}{2}}\Rightarrow \frac{A\left(0\right)}{A\left(\frac{1}{2}\right)}=2\sqrt[]{2}$}

$area=2*\left(\frac{1}{2}*1*1\right)=1=k$