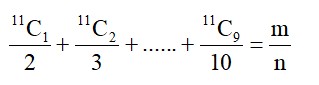Let "Cᵣ denote the binomial coefficient of xʳ in the expansion of (1+x)ⁿ. If Σₖ₌₀¹⁰ (2² + 3k) ⁿCₖ = α.3¹⁰ + β.2¹⁰, α,β ∈ R, then α + β is equal to......

${\left(1+x\right)}^{11}={}^{11}{C}_0+{}^{11}{C}_{1}x+{}^{11}{C}_2{x}^2+.....{+}^{11}{C}_{11}{x}^{11}$

$=\frac{2^{12}-2-24}{12}$

$=\frac{2^{12}-26}{12}=\frac{4070}{12}=\frac{2035}{6}=\frac{m}{n}$

m + n = 2035 + 6 = 2041

$T_{n+1}={}^n{C}_{r}11^{\frac{1}{6}}\cdot 7^{\frac{824-4}{2}}$

For integral term

6 should divide r

and  $\frac{824-r}{2}$  must be integer

->2 most divide r

->r divisible by 6

->possible values of r Î {0, 1, 2, …824}

->For integer terms

r Î {0, 6, 12, …822} (822 = 0 + (n – 1)6 Þ n = 138)

= 138 terms

The common mistakes can be - using the formula incorrectly, before applying the formula students not simplify the expression, in Binomial Expansion, sometimes they forget to include the fractional and negative exponents, and using incorrect values for a, b, and n.

The Binomial model is known as the Lattice Model or Binomial Option Pricing Model.

There are a total of 36 questions comprising 14 straightforward formula-based sums, 16 challenging problems, and 6 intermediate.