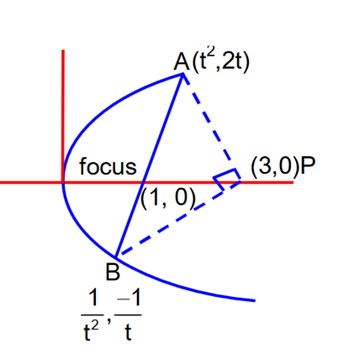
Let PQ be a focal chord of the parabola y2 = 4x such that it subtends an angle of at the point (3, 0). Let the line segment PQ be also a focal chord of the ellipse E: If e is the eccentricity of the ellipse E, then the value of is equal to:
Let PQ be a focal chord of the parabola y2 = 4x such that it subtends an angle of at the point (3, 0). Let the line segment PQ be also a focal chord of the ellipse E: If e is the eccentricity of the ellipse E, then the value of is equal to:
Option 1 -
Option 2 -
Option 3 -
Option 4 -
-
1 Answer
-
Correct Option - 2
Detailed Solution:M1 M2 = 1
t = 1
So, A (1, 2) and B (1, 2) they must be end pts of focal chord.
Length of latus rectum
b2 = 2a and ae = 1
Eccentricity of ellipse (Horizontal)
b2 = a2 (1 – e2)
2a = a2 (1 – e2)
2 =
e2 + 2e – 1 = 0
now
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers