Let S = {1, 2, 3, 4, 5, 6, 7}. Then the number of possible function f: S → S such that f(m.n) = f(m).f(n) for every m, n ∈ S and m.n ∈ S is equal to ________.

R₁ = { (1, 1) (1, 2), (1, 3)., (1, 20), (2, 2), (2, 4). (2, 20), (3, 3), (3, 6), . (3, 18),
(4, 4), (4, 8), . (4, 20), (5, 5), (5, 10), (5, 15), (5, 20), (6, 6), (6, 12), (6, 18), (7. 7),
(7, 14), (8, 8), (8, 16), (9, 9), (9, 18), (10, 10), (10, 20), (11, 11), (12, 12), . (20, 20)}

n (R₁) = 66

R₂ = {a is integral multiple of b}

So n (R₁ – R₂) = 66 – 20 = 46

as R₁ Ç R₂ = { (a, a) : a Î s} = { (1, 1), (2, 2), ., (20, 20)}

$gof\left(x\right)=\{\begin{array}{cc}\hfill f\left(x\right),\hfill & \hfill f\left(x\right)<0\hfill \\ \hfill f\left(x\right),\hfill & \hfill f\left(x\right)>0\hfill \end{array}$

$=\{\begin{array}{lll}{e}^{lnx}=x\hfill & \left(0,1\right)\hfill & e^{-x}\hfill \\ \left(-\infty ,0\right)\hfill & lnx\hfill & \left(1,\infty \right)\hfill \end{array}$

Therefore, gof (x) is many one and into

  $?$  R is symmetric relation

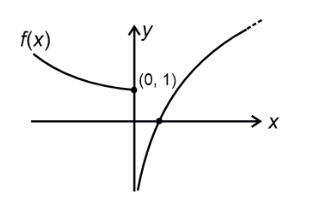
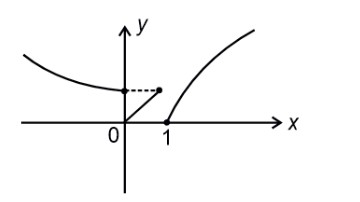
⇒   (y, x) ∈ R V (x, y) ∈ R

(x, y) ∈ R ⇒ 2x = 3y and (y, x) ∈ R ⇒ 3x = 2y

Which holds only for (0, 0)

Which does not belongs to R.

∴ Value of n = 0

f is increasing function

x < 5x < 7x

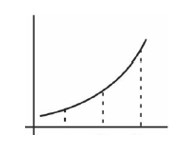
f (x) < f (5x) < f (7x)

  $\frac{f\left(x\right)}{f\left(x\right)}<\frac{f\left(5x\right)}{f\left(x\right)}<\frac{f\left(7x\right)}{f\left(x\right)}$           

$\underset{x\to \infty }{lim}\frac{f\left(x\right)}{f\left(x\right)}<\underset{x\to \infty }{lim}\frac{f\left(5x\right)}{f\left(x\right)}<\underset{x\to \infty }{lim}\frac{f\left(7x\right)}{f\left(x\right)}$             

-> $1<\underset{x\to \infty }{lim}\frac{f\left(5x\right)}{f\left(x\right)}<1$ $\underset{x\to \infty }{lim}\frac{f\left(5x\right)}{f\left(x\right)}=1$

$\underset{x\to \infty }{lim}\left(\frac{f\left(5x\right)}{f\left(x\right)}-1\right)=0$            

Given f (k) = $\{\begin{array}{l}k+1,kisodd\\ k,kiseven\end{array}$

  $?g:A\to A$           such that g (f (x) = f (x)

Case I : If x is even then g (x) = x . (i)

Case II : If x is odd then g (x + 1) = x + 1 . (ii)

From (i) & (ii), g (x) = x, when x is even

So total no. of functions = 10⁵ × 1 = 10⁵