Let S = [1, 2, 3, 4, 5, 6, 9]. Then the number of elements in the set T
and the sum of all the elements of A is not a multiple of 3} is____
Let S = [1, 2, 3, 4, 5, 6, 9]. Then the number of elements in the set T and the sum of all the elements of A is not a multiple of 3} is____
-
1 Answer
-
S = {1, 2, 3, 4, 5, 6, 9}
Elements of type 3n -> 3, 6, 9
Type 3n + 1 ->1, 4
3n + 2 -> 2, 5
Number of subset of S containing one element which are not divisible by
Number of subset of S containing 3 elements whose sum is not divisible by
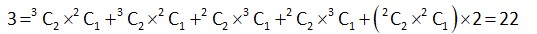
Number of subset containing 4 elements whose sum is not divisible by 3
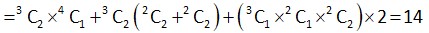
Number of subset of S containing 6 elements = 4
Hence total subset = 80
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers
