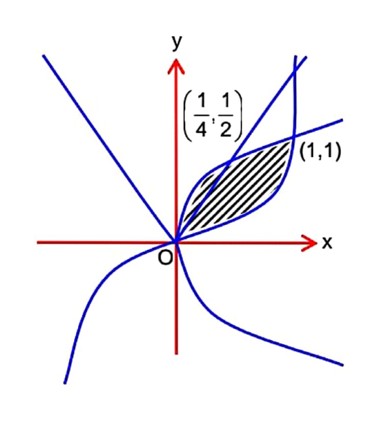
Let S be the region bonded by the curves y = x³ and y² = x. The curve y = 2|x| divides S into two regions of areas R₁, and R₂ _________.

If max {R₁, R₂} = R₂, then $\frac{R_2}{R_1}$  is equal to _________.

$y^2=x,a=\frac{1}{4}$

$x^2=-y,b=\frac{1}{4}$

$A=\frac{16\left|ab\right|}{3}=\frac{1}{3}$

A = ∫? ² lnx dx = 2ln2 – 1
A' = 4 - 2 (2ln2 – 1) = 6 – 4ln2

y = |x − 1|, y = 3 – |x|

(A graph is shown with vertices A (1, 0), B (2, 1), C (0, 3), D (-1, 2). The lines are y = x - 1, y = 3 - x, y = 3 + x, and y = -x + 1)

AB = √2, BC = 2√2
⇒ Area = 4 sq. units

Required area (above x-axis)
A? = 2∫? (8/2 - x - √x)dx
= 2 [16 - 16/4 - 8/3*2] = 40/3
and A? = 4 (1/2 k²) = 2k²

∴ 27 * (40/3) = 5 * (2k²)
=> k = 6
for above x-axis.

We are given bounds for a function f (t) on two intervals and need to find the range of g (3) = ∫? ³ f (t) dt.
We split the integral: g (3) = ∫? ¹ f (t)dt + ∫? ³ f (t)dt.
For the first interval t ∈ [0, 1], we have 1/3 ≤ f (t) ≤ 1. Integrating from 0 to 1 gives:
∫? ¹ (1/3) dt ≤ ∫? ¹ f (t)dt ≤ ∫? ¹ 1 dt